题目内容
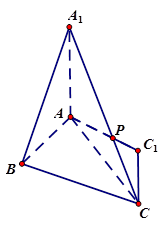
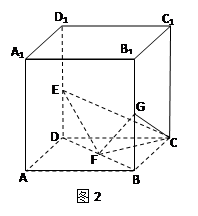
(本小题满分12分)如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°。
(1)证明:平面ADB⊥平面BDC;
(2 )设BD=1,求三棱锥D—ABC的表面积。

(1)证明:平面ADB⊥平面BDC;
(2 )设BD=1,求三棱锥D—ABC的表面积。

20.【解】(1)∵折起前AD是BC边上的高,
∴ 当Δ ABD折起后,AD⊥DC,AD⊥DB,………2分
又DB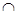 DC=D,…………3分
DC=D,…………3分
∴AD⊥平面BDC,又∵AD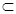 面ABD
面ABD
…………………………………5分
∴平面ABD⊥平面BDC.………6分
(2)由(1)知,DA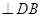 ,
,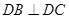 ,
,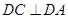 ,
,
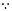 DB=DA=DC=1,
DB=DA=DC=1,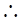 AB=BC=CA=
AB=BC=CA= ,
,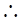
 ……7分
……7分

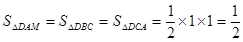 ,
,
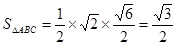 ………10分
………10分
∴三棱锥D—ABC的表面积是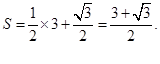 ………………12分
………………12分
∴ 当Δ ABD折起后,AD⊥DC,AD⊥DB,………2分
又DB
 DC=D,…………3分
DC=D,…………3分∴AD⊥平面BDC,又∵AD
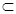 面ABD
面ABD…………………………………5分
∴平面ABD⊥平面BDC.………6分
(2)由(1)知,DA
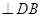 ,
,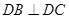 ,
,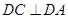 ,
,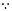 DB=DA=DC=1,
DB=DA=DC=1,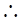 AB=BC=CA=
AB=BC=CA= ,
,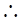
 ……7分
……7分
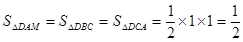 ,
,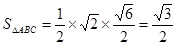 ………10分
………10分∴三棱锥D—ABC的表面积是
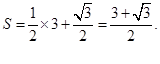 ………………12分
………………12分略

练习册系列答案
相关题目
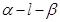 的大小为
的大小为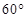 ,点
,点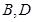 棱
棱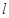 上,
上,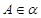 ,
,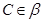 ,
,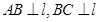 ,
,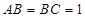 ,
,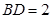 ,则异面直线
,则异面直线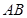 与
与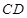 所成角的余弦值为
所成角的余弦值为



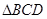 的( )
的( )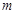 、
、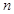 、
、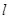 不重合,平面
不重合,平面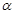 、
、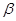 不重合,下列命题正确的是 ( )
不重合,下列命题正确的是 ( ) ,
, ,
, ,则
,则
 ,则
,则
 ,则
,则
 ,则
,则
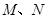 分别是
分别是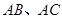 的中点,
的中点,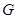 是
是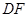 上的一动点.
上的一动点.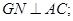
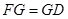 时,在棱
时,在棱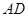 上确定一点
上确定一点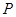 ,使得
,使得 //平面
//平面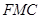 ,并给出证明.
,并给出证明. 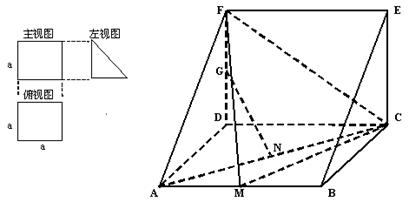
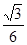

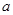 、
、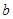 ,
,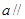 平面
平面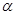 ,则
,则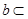 平面
平面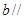 平面
平面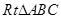 中,
中,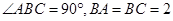 ,分别过
,分别过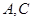 作平面
作平面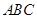 的垂线
的垂线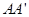 和
和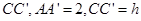 ,连结
,连结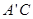 和
和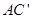 交于点
交于点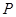 .
.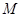 为
为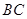 中点,若
中点,若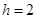 ,求证:直线
,求证:直线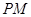 与平面
与平面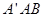 平行;
平行;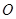 为
为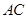
 中点,二面角
中点,二面角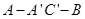 等于
等于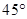 ,求直线
,求直线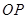 与平面
与平面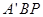 所成角
所成角