ЬтФПФкШн
ЁОЬтФПЁПФГЙЋЫОЮЊзЅзЁОМУЗЂеЙЕФЦѕЛњЃЌЕїВщСЫНтСЫНќМИФъЙуИцЭЖШыЖдЯњЪлЪевцЕФгАЯьЃЌдкШєИЩЯњЪлЕиЧјЗжБ№ЭЖШы4ЭђдЊЙуИцЗбгУЃЌВЂНЋИїЕиЕФЯњЪлЪевцЛцжЦГЩЦЕТЪЗжВМжБЗНЭМЃЈШчЭМЫљЪОЃЉЃЌгЩгкЙЄзїШЫдБВйзїЪЇЮѓЃЌКсжсЕФЪ§ОнЖЊЪЇЃЌЕЋПЩвдШЗЖЈКсжсЪЧДг0ПЊЪММЦЪ§ЕФ.
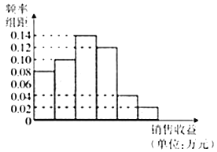
ЃЈ1ЃЉИљОнЦЕТЪЗжВМжБЗНЭММЦЫуЭМжаИїаЁГЄЗНаЮЕФПэЖШЃЛВЂЙРМЦИУЙЋЫОЗжБ№ЭЖШы4ЭђдЊЙуИцЗбгУжЎКѓЃЌЖдгІЕиЧјЯњЪлЪевцЕФЦНОљжЕЃЈвдИїзщЕФЧјМфжаЕужЕДњБэИУзщЕФШЁжЕЃЉЃЛ
ЃЈ2ЃЉИУЙЋЫОАДееРрЫЦЕФбаОПЗНЗЈЃЌВтЕУСэЭтвЛаЉЪ§ОнЃЌВЂећРэЕУЕНШчБэЃК
ЙуИцЭЖШыxЃЈЕЅЮЛЃКЭђдЊЃЉ | 1 | 2 | 3 | 4 | 5 |
ЯњЪлЪевцyЃЈЕЅЮЛЃКЭђдЊЃЉ | 2 | 3 | 2 | 7 |
гЩБэжаЕФЪ§ОнЯдЪОЃЌxгыyжЎМфДцдкзХЯпадЯрЙиЙиЯЕЃЌЧыНЋЃЈ1ЃЉЕФНсЙћЬюШыПеАзРИЃЌИљОнБэИёжаЪ§ОнЧѓГіyЙигкxЕФЛиЙщецЯпЗНГЬ![]() ЃЌВЂЙРМЦИУЙЋЫОЯТвЛФъЭЖШыЙуИцЗбЖрЩйЭђдЊЪБЃЌПЩЪЙЕУЯњЪлЪевцДяЕН8ЭђдЊЃП
ЃЌВЂЙРМЦИУЙЋЫОЯТвЛФъЭЖШыЙуИцЗбЖрЩйЭђдЊЪБЃЌПЩЪЙЕУЯњЪлЪевцДяЕН8ЭђдЊЃП
ВЮПМЙЋЪНЃКзюаЁЖўГЫЗЈЙРМЦЗжБ№ЮЊ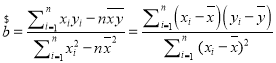 ЃЌ
ЃЌ![]() .
.
ЁОД№АИЁПЃЈ1ЃЉПэЖШЮЊЃК2ЃЌ ЦНОљжЕЃК5ЃЈ2ЃЉПеАзРИжаЬю5ЃЌ![]() ЃЌЭЖШы
ЃЌЭЖШы![]() ЭђдЊ
ЭђдЊ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЦЕТЪЗжВМжБЗНЭМИїИіаЁГЄЗНаЮЕФУцЛ§змКЭЮЊ1ЃЌНЈСЂЗНГЬЃЌМДПЩЧѓЕУНсТл.РћгУзщжажЕЃЌЧѓГіЖдгІЯњЪлЪевцЕФЦНОљжЕЃЛ
ЃЈ2ЃЉРћгУЙЋЪНЧѓГі![]() МДПЩМЦЫуyЙигкxЕФЛиЙщЗНГЬ.
МДПЩМЦЫуyЙигкxЕФЛиЙщЗНГЬ.
ЃЈ1ЃЉЩшГЄЗНаЮЕФПэЖШЮЊmЃЌгЩЦЕТЪЗжВМжБЗНЭМИїаЁГЄЗНаЮУцЛ§змКЭЮЊ1ЃЌ
ПЩжЊЃЈ0.08+0.1+0.14+0.12+0.04+0.02ЃЉmЃН1ЃЌЫљвдmЃН2.
аЁзщвРДЮЪЧ[0ЃЌ2ЃЉЃЌ[2ЃЌ4ЃЉЃЌ[4ЃЌ6ЃЉЃЌ[6ЃЌ8ЃЉЃЌ[8ЃЌ10ЃЉЃЌ[10ЃЌ12ЃЉЃЌ
ЦфжаЕуЗжБ№ЮЊ1ЃЌ3ЃЌ5ЃЌ7ЃЌ9.11
ЖдгІЕФЦЕТЪЗжБ№ЮЊ0.16ЃЌ0.20ЃЌ0.28ЃЌ0.24ЃЌ0.08ЃЌ0.04.
ЙЪПЩЙРМЦЦНОљжЕЮЊ1ЁС0.16+3ЁС0.20+5ЁС028+7ЁС0.24+9ЁС0.08+11ЁС0.04ЃН5.
ЃЈ2ЃЉПеАзРИжаЬю5.
гЩЬтвтПЩжЊЃЌ![]() 3ЃЌ
3ЃЌ![]() 3.8ЃЌ
3.8ЃЌ![]() 69ЃЌ
69ЃЌ![]() 55ЃЌ
55ЃЌ
Ыљвд![]() 1.2ЃЌ
1.2ЃЌ![]() 3.8Љ1.2ЁС3ЃН0.2.
3.8Љ1.2ЁС3ЃН0.2.
ЫљвдЙигкxЕФЛиЙщЗНГЬЮЊ![]()
ШЁ![]() ЃЌЕУЕН
ЃЌЕУЕН![]() .
.