题目内容
【题目】已知定义在[0,1]上的函数f(x)满足:
①f(0)=f(1)=0;
②对所有x,y∈[0,1],且x≠y,有|f(x)﹣f(y)|< ![]() |x﹣y|.
|x﹣y|.
若对所有x,y∈[0,1],|f(x)﹣f(y)|<m恒成立,则m的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:依题意,定义在[0,1]上的函数y=f(x)的斜率|k|< ![]() ,
,
依题意可设k>0,构造函数f(x)= 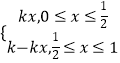 (0<k<
(0<k< ![]() ),满足f(0)=f(1)=0,|f(x)﹣f(y)|<
),满足f(0)=f(1)=0,|f(x)﹣f(y)|< ![]() |x﹣y|.
|x﹣y|.
当x∈[0, ![]() ],且y∈[0,
],且y∈[0, ![]() ]时,|f(x)﹣f(y)|=|kx﹣ky|=k|x﹣y|≤k|
]时,|f(x)﹣f(y)|=|kx﹣ky|=k|x﹣y|≤k| ![]() ﹣0|=k×
﹣0|=k× ![]() <
< ![]() ;
;
当x∈[0, ![]() ],且y∈[
],且y∈[ ![]() ,1],|f(x)﹣f(y)|=|kx﹣(k﹣ky)|=|k(x+y)﹣k|≤|k(1+
,1],|f(x)﹣f(y)|=|kx﹣(k﹣ky)|=|k(x+y)﹣k|≤|k(1+ ![]() )﹣k|=
)﹣k|= ![]() <
< ![]() ;
;
当y∈[0, ![]() ],且x∈[
],且x∈[ ![]() ,1]时,同理可得,|f(x)﹣f(y)|<
,1]时,同理可得,|f(x)﹣f(y)|< ![]() ;
;
当x∈[ ![]() ,1],且y∈[
,1],且y∈[ ![]() ,1]时,|f(x)﹣f(y)|=|(k﹣kx)﹣(k﹣ky)|=k|x﹣y|≤k×(1﹣
,1]时,|f(x)﹣f(y)|=|(k﹣kx)﹣(k﹣ky)|=k|x﹣y|≤k×(1﹣ ![]() )=
)= ![]() <
< ![]() ;
;
综上所述,对所有x,y∈[0,1],|f(x)﹣f(y)|< ![]() ,
,
∵对所有x,y∈[0,1],|f(x)﹣f(y)|<m恒成立,
∴m≥ ![]() ,即m的最小值为
,即m的最小值为 ![]() .
.
故选:B.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
【题目】某校高三年级共有学生![]() 名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为
名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为![]() 分)进行统计,绘制出如下尚未完成的频率分布表:
分)进行统计,绘制出如下尚未完成的频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
| |
| ||
|
|
(1)补充完整题中的频率分布表;
(2)若成绩在![]() 为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.