Question

【题目】如图，公路AM，AN围成一块顶角为α的角形耕地，其中tanα＝－2，在该块土地中P处有一小型建筑，经测量，它到公路AM，AN的距离分别为3km，km，现要过点P修建一条直线公路BC，将三条公路围成的区域ABC建成一个工业园，为尽量减少耕地占用，问如何确定B点的位置，使得该工业园区的面积最小？并求最小面积．

Answer 1

【答案】当AB＝5km时，该工业园区的面积最小，最小面积为15km2．

【解析】

试题分析：先确定点P的位置，再利用BC的斜率表示工业园区的面积，利用导数求其最值.以A为原点，AB为x轴，建立平面直角坐标系．因为tanα＝－2，故直线AN的方程是y＝－2x．设点P(x0，y0)．因为点P到AM的距离为3，故y0＝3．由P到直线AN的距离为，得，解得x0＝1或x0＝－4(舍去)，所以点P(1，3)．显然直线BC的斜率存在．设直线BC的方程为y－3＝k(x－1)，k∈(－2，0)．令y＝0得xB＝1－．由解得yC＝．设△ABC的面积为S，则S＝xB×yC＝．由S＝＝0得k＝－或k＝3．所以当k＝－时，即AB＝5时，S取极小值，也为最小值15．

试题解析：解：如图1，以A为原点，AB为x轴，建立平面直角坐标系．因为tanα＝－2，故直线AN的方程是y＝－2x．

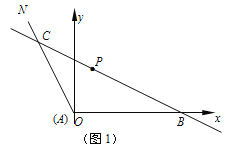
设点P(x0，y0)．

因为点P到AM的距离为3，故y0＝3．

由P到直线AN的距离为，

得，解得x0＝1或x0＝－4(舍去)，

所以点P(1，3)． 4分

显然直线BC的斜率存在．设直线BC的方程为y－3＝k(x－1)，k∈(－2，0)．

令y＝0得xB＝1－． 6分

由解得yC＝． 8分

设△ABC的面积为S，则S＝×xB×yC＝10分

由S＝＝0得k＝－或k＝3．

当－2＜k＜－时，S＜0，S单调递减；当－＜k＜0时，S＞0，S单调递增． 13分

所以当k＝－时，即AB＝5时，S取极小值，也为最小值15．

答：当AB＝5km时，该工业园区的面积最小，最小面积为15km2． 16分