题目内容
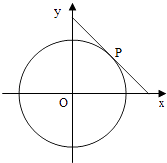
【题目】圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线C1: ![]() 过点P且离心率为
过点P且离心率为 ![]() .
. 
(1)求C1的方程;
(2)若椭圆C2过点P且与C1有相同的焦点,直线l过C2的右焦点且与C2交于A,B两点,若以线段AB为直径的圆过点P,求l的方程.
【答案】
(1)解:设切点P(x0,y0),(x0>0,y0>0),则切线的斜率为 ![]() ,
,
可得切线的方程为 ![]() ,化为x0x+y0y=4.
,化为x0x+y0y=4.
令x=0,可得 ![]() ;令y=0,可得
;令y=0,可得 ![]() .
.
∴切线与x轴正半轴,y轴正半轴围成一个三角形的面积S= ![]() =
= ![]() .
.
∵4= ![]() ,当且仅当
,当且仅当 ![]() 时取等号.
时取等号.
∴ ![]() .此时P
.此时P ![]() .
.
由题意可得 ![]() ,
, ![]() ,解得a2=1,b2=2.
,解得a2=1,b2=2.
故双曲线C1的方程为 ![]() .
.
(2)解:由(1)可知双曲线C1的焦点(± ![]() ,0),即为椭圆C2的焦点.
,0),即为椭圆C2的焦点.
可设椭圆C2的方程为 ![]() (b1>0).
(b1>0).
把P ![]() 代入可得
代入可得 ![]() ,解得
,解得 ![]() =3,
=3,
因此椭圆C2的方程为 ![]() .
.
由题意可设直线l的方程为x=my+ ![]() ,A(x1,y1),B(x2,y2),
,A(x1,y1),B(x2,y2),
联立 ![]() ,化为
,化为 ![]() ,
,
∴ ![]() ,
, ![]() .
.
∴x1+x2= ![]() =
= ![]() ,
,
x1x2= ![]() =
= ![]() .
.
![]() ,
, ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() +
+ ![]() ,
,
∴ ![]() ,解得m=
,解得m= ![]() -1或m=
-1或m= ![]() ,
,
因此直线l的方程为: ![]() 或
或 ![]()
【解析】(1)设切点P(x0 , y0),(x0>0,y0>0),利用相互垂直的直线斜率之间的关系可得切线的斜率和切线的方程,即可得出三角形的面积,利用基本不等式的性质可得点P的坐标,再利用双曲线的标准方程及其性质即可得出;(2)由(1)可得椭圆C2的焦点.可设椭圆C2的方程为 ![]() (b1>0).把P的坐标代入即可得出方程.由题意可设直线l的方程为x=my+
(b1>0).把P的坐标代入即可得出方程.由题意可设直线l的方程为x=my+ ![]() ,A(x1 , y1),B(x2 , y2),与椭圆的方程联立即可得出根与系数的关系,再利用向量垂直与数量积的关系即可得出.
,A(x1 , y1),B(x2 , y2),与椭圆的方程联立即可得出根与系数的关系,再利用向量垂直与数量积的关系即可得出.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案【题目】某高级中学共有学生2000名,各年级男、女生人数如下表:
高一年级 | 高二年级 | 高三年级 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(1)求![]() 的值;
的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应该在高三年级抽取多少名?
(3)已知![]() ,
,![]() ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率.



