题目内容
如图,在直三棱柱ABC—A1B1C1中,∠ABC=90°,AB=BC=AA1=2,M、N分别是A1C1、BC1的中点.
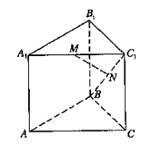
(I)求证:BC1⊥平面A1B1C;
(II)求证:MN∥平面A1ABB1;
(III)求多面体M—BC1B1的体积.

(I)求证:BC1⊥平面A1B1C;
(II)求证:MN∥平面A1ABB1;
(III)求多面体M—BC1B1的体积.
(I)(II)见解析(Ⅲ)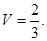
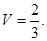
(I)∵直三棱柱ABC—A1B1C1,
∴B1B⊥面A1B1C1. 1分
∴B1B⊥A1B1.
又∵A1B1⊥B1C1,
∴A1B1⊥面BCC1B1.
∴A1B1⊥BC1,
连结B1C,∵矩形BCC1B1中,BB1=CB=2,
∴BC1⊥B1C,
∴B1C⊥平面A1B1C. 5分
(II)连结A1B,由M、N分别为A1C1、BC1的中点可得,
MN∥A1B
又∵A1B1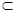 平面A1ABB1,MN
平面A1ABB1,MN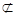 平面A1ABB1,
平面A1ABB1,
∴MN∥平面A1ABB1. 10分
(III)取C1B1中点H,连结MH、MB1、MB,
又∵M是A1C1中点,
∴MH∥A1B1,
又∵A1B1⊥平面BBC1B1,
∴MH⊥平面BCC1B1,
∴三棱锥M—BC1B1以MH为高,△BC1B1为底面,
三棱锥M—BC1B1的体积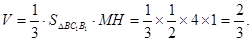 14分
14分
∴B1B⊥面A1B1C1. 1分
∴B1B⊥A1B1.
又∵A1B1⊥B1C1,
∴A1B1⊥面BCC1B1.
∴A1B1⊥BC1,
连结B1C,∵矩形BCC1B1中,BB1=CB=2,
∴BC1⊥B1C,
∴B1C⊥平面A1B1C. 5分
(II)连结A1B,由M、N分别为A1C1、BC1的中点可得,
MN∥A1B
又∵A1B1
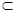 平面A1ABB1,MN
平面A1ABB1,MN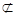 平面A1ABB1,
平面A1ABB1,∴MN∥平面A1ABB1. 10分
(III)取C1B1中点H,连结MH、MB1、MB,
又∵M是A1C1中点,
∴MH∥A1B1,
又∵A1B1⊥平面BBC1B1,
∴MH⊥平面BCC1B1,
∴三棱锥M—BC1B1以MH为高,△BC1B1为底面,
三棱锥M—BC1B1的体积
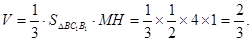 14分
14分
练习册系列答案
相关题目
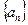 中,已知a1=2,an+1=4an-3n+1,n∈
中,已知a1=2,an+1=4an-3n+1,n∈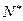 .
.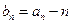 ,求数列
,求数列 的通项公式;
的通项公式;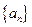 的各项均为正数,观察下面程序框图,当
的各项均为正数,观察下面程序框图,当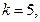
 时,分别
时,分别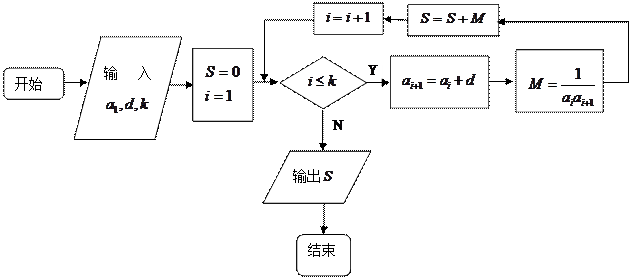
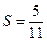 和
和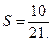 .
.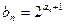 ,
,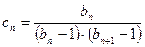
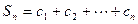 求证:
求证: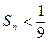 .
.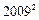
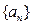 的前n项和
的前n项和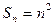 ,
, 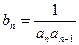 ,求数列
,求数列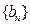 的前n项和
的前n项和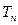 .
.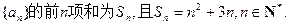
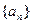 的通项公式; (II)求数列
的通项公式; (II)求数列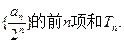
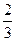 ,且
,且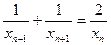 (n≥2),则xn等于( )
(n≥2),则xn等于( )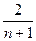
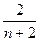
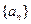
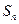
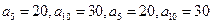
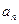 ; (2)若
; (2)若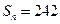 ,求n
,求n