题目内容
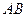
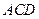
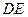
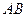
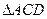
正三角形,
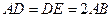 ,且
,且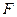 是
是 的中点.
的中点.(Ⅰ)求证:
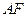 ∥平面
∥平面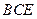 ;
;(Ⅱ)求证:平面BCE⊥平面
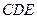 .
.
见解析
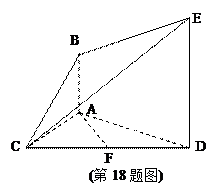
(Ⅰ)取CE中点P,连结FP、BP,
∵F为CD的中点,
∴FP∥DE,且FP=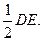
又AB∥DE,且AB=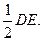
 ∴AB∥FP,且AB=FP,
∴AB∥FP,且AB=FP,
∴ABPF为平行四边形,∴AF∥BP.…………4分
又∵AF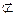 平面BCE,BP
平面BCE,BP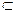 平面BCE,
平面BCE,
∴AF∥平面BCE…………6分
(Ⅱ)∵△ACD为正三角形,∴AF⊥CD
∵AB⊥平面ACD,DE//AB
∴DE⊥平面ACD 又AF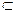 平面ACD
平面ACD
∴DE⊥AF
又AF⊥CD,CD∩DE=D
∴AF⊥平面CDE …………10分
又BP∥AF ∴BP⊥平面CDE
又∵BP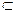 平面BCE
平面BCE
∴平面BCE⊥平面CDE …………12分
∵F为CD的中点,
∴FP∥DE,且FP=
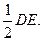
又AB∥DE,且AB=
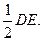
 ∴AB∥FP,且AB=FP,
∴AB∥FP,且AB=FP,∴ABPF为平行四边形,∴AF∥BP.…………4分
又∵AF
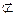 平面BCE,BP
平面BCE,BP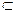 平面BCE,
平面BCE,∴AF∥平面BCE…………6分
(Ⅱ)∵△ACD为正三角形,∴AF⊥CD
∵AB⊥平面ACD,DE//AB
∴DE⊥平面ACD 又AF
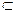 平面ACD
平面ACD∴DE⊥AF
又AF⊥CD,CD∩DE=D
∴AF⊥平面CDE …………10分
又BP∥AF ∴BP⊥平面CDE
又∵BP
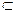 平面BCE
平面BCE∴平面BCE⊥平面CDE …………12分

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
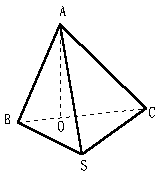
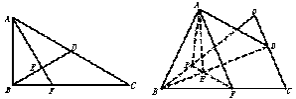
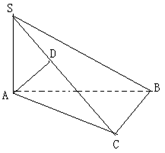
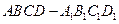 中,点
中,点 ,
,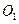 分别是四边形
分别是四边形 ,
,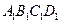 的对角线的交点,点
的对角线的交点,点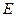 ,
,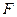 分别是四边形
分别是四边形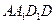 ,
,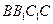 的对角线的交点,点
的对角线的交点,点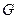 ,
,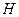 分别是四边形
分别是四边形 ,
,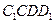 的对角线的交点.求证:
的对角线的交点.求证: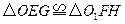 .
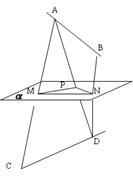
.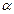 ,且AB、CD在
,且AB、CD在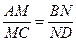 。
。
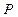
 (2)若F为侧棱PA上的一点,且
(2)若F为侧棱PA上的一点,且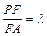 , 则为何值时,PA平面BDF? 并求此时几何体F—BDC的体积.
, 则为何值时,PA平面BDF? 并求此时几何体F—BDC的体积.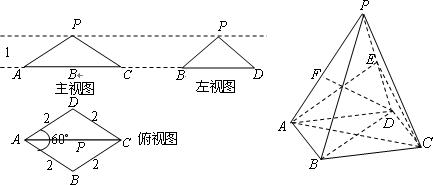


 .
.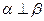 ,
,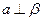 ,
,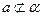 ;求证:
;求证: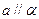 .
. 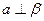 ,
,