题目内容
8.将函数f1(x)=sinx与函数f2(x)=cosx线性组构成的函数f(x)=Af1(x)+Bf2(x)(A,B是常数,x∈R)图象称为(A,B)曲线.(1)若(A,B)曲线经过点P($\frac{π}{3}$,0),Q(π,-2$\sqrt{3}$),求A、B的值;
(2)若(A,B)曲线与射线y=2(x≥0)的所有交点的横坐标依次组成一个等差数列{an},且a1=$\frac{π}{3}$,求数列{an}的通项以及常数A、B的值;
(3)在(1)的条件下,求证:对x∈(0,+∞),恒有f(x)>-x-$\frac{2π}{3}$.
分析 (1)由题意知f(x)=Asinx+Bcosx,从而可得f($\frac{π}{3}$)=Asin$\frac{π}{3}$+Bcos$\frac{π}{3}$=0,f(π)=Asinπ+Bcosπ=-2$\sqrt{3}$;从而解得;
(2)由题意知函数f(x)=Asinx+Bcosx的最大值为2;从而可得f($\frac{π}{3}$)=Asin$\frac{π}{3}$+Bcos$\frac{π}{3}$=2,A2+B2=4;从而解得;
(3)由(1)得,f(x)=-2sinx+2$\sqrt{3}$cosx=4sin(x+$\frac{2π}{3}$);从而化简为4sin(x+$\frac{2π}{3}$)+x+$\frac{2π}{3}$>0在(0,+∞)上恒成立,即证4sinx+x>0在($\frac{2π}{3}$,+∞)上恒成立;从而证明即可.
解答 解:(1)由题意,f(x)=Asinx+Bcosx,
则f($\frac{π}{3}$)=Asin$\frac{π}{3}$+Bcos$\frac{π}{3}$=0,
f(π)=Asinπ+Bcosπ=-2$\sqrt{3}$;
解得,A=-2,B=2$\sqrt{3}$;
(2)由函数f(x)=Asinx+Bcosx的图象与射线y=2(x≥0)的所有交点的横坐标依次组成一个等差数列{an}知,
函数f(x)=Asinx+Bcosx的最大值为2;
则f($\frac{π}{3}$)=Asin$\frac{π}{3}$+Bcos$\frac{π}{3}$=2,
A2+B2=4;
解得,A=$\sqrt{3}$,B=1;
故f(x)=$\sqrt{3}$sinx+cosx=2sin(x+$\frac{π}{6}$),
T=2π;
故数列{an}的通项an=$\frac{π}{3}$+(n-1)2π=2nπ-$\frac{5}{3}π$;
(3)证明:由(1)得,f(x)=-2sinx+2$\sqrt{3}$cosx=4sin(x+$\frac{2π}{3}$);
故f(x)>-x-$\frac{2π}{3}$可化为4sin(x+$\frac{2π}{3}$)+x+$\frac{2π}{3}$>0,
故原命题可化为4sin(x+$\frac{2π}{3}$)+x+$\frac{2π}{3}$>0在(0,+∞)上恒成立,
即证4sinx+x>0在($\frac{2π}{3}$,+∞)上恒成立;
①当x>4时,4sinx+x>0一定成立;
②当$\frac{2π}{3}$<x≤4时,
令g(x)=4sinx+x,
g′(x)=4cosx+1,
∵$\frac{2π}{3}$<x≤4<$\frac{4π}{3}$;
∴g′(x)=4cosx+1<0,
∴g(x)=4sinx+x在($\frac{2π}{3}$,4]上是减函数,
故g(x)≥g(4)=4sin4+4>0;
综上所述,对x∈(0,+∞),恒有f(x)>-x-$\frac{2π}{3}$.
点评 本题考查了三角函数的性质应用及数列的应用,同时考查了分类讨论的思想应用及恒成立问题,导数的综合应用,属于难题.

]与函数g(x)=ax2+bx的图象恰有1个公共点,则a,b的取值不可能是( )
| A. | a=5,b=1 | B. | a=4,b=-1 | C. | a=-2,b=-1 | D. | a=-4,b=1 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
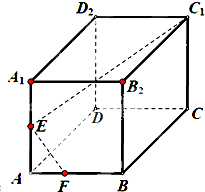
 如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAC=90°,AB=$\sqrt{3}$,BC=1,AD=AA1=3.
如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAC=90°,AB=$\sqrt{3}$,BC=1,AD=AA1=3.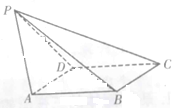 如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BAD=60°.
如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BAD=60°.