题目内容
【题目】(本题满分12分)已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的x轴的正半轴重合,且两个坐标系的单位长度相同.已知直线l的参数方程为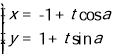 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为![]() .
.
(Ⅰ)若直线l的斜率为-1,求直线l与曲线C交点的极坐标;
(Ⅱ)若直线l与曲线C相交弦长为![]() ,求直线l的参数方程(标准形式).
,求直线l的参数方程(标准形式).
【答案】(Ⅰ)![]() ;
;
(Ⅱ)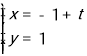 (
(![]() 为参数)或
为参数)或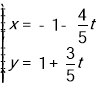 (
(![]() 为参数)
为参数)
【解析】
试题分析:(Ⅰ)由直线![]() 的参数方程可知其过定点
的参数方程可知其过定点![]() ,从而由直线方程的点斜式可得直线
,从而由直线方程的点斜式可得直线![]() 的普通方程,将曲线
的普通方程,将曲线![]() 的极坐标方程按照极坐标和直角坐标互化公式
的极坐标方程按照极坐标和直角坐标互化公式![]() 将其化为直角坐标方程,然后将直线方程和曲线方程联立求交点的直角作标,再将其化为极坐标. (Ⅱ)设出直线的斜率写出直线方程的直角坐标方程,由(Ⅰ)知曲线
将其化为直角坐标方程,然后将直线方程和曲线方程联立求交点的直角作标,再将其化为极坐标. (Ⅱ)设出直线的斜率写出直线方程的直角坐标方程,由(Ⅰ)知曲线![]() 时圆心为
时圆心为![]() 半径为
半径为![]() 的圆.先求圆心到直线的距离,再根据勾股定理可得关于
的圆.先求圆心到直线的距离,再根据勾股定理可得关于![]() 的方程,从而可求得
的方程,从而可求得![]() 的值.即可知直线的倾斜角,从而可得直线的参数方程.
的值.即可知直线的倾斜角,从而可得直线的参数方程.
试题解析:解:(Ⅰ)直线![]() 的方程:
的方程:![]() ,即
,即![]() ;(1分)
;(1分)
![]() ,即
,即![]() ,(2分)
,(2分)
联立方程得![]() ,∴
,∴![]() ;(4分)
;(4分)
极坐标为![]() ;(5分)
;(5分)
(Ⅱ)![]() ,弦心距
,弦心距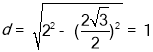 ,(6分)
,(6分)
设直线l的方程为![]() ,∴
,∴![]() ,∴
,∴![]() 或
或![]() .(8分)
.(8分)
∴直线![]() :
: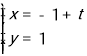 (
(![]() 为参数)或
为参数)或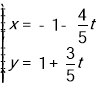 (
(![]() 为参数)(10分)
为参数)(10分)

练习册系列答案
相关题目