题目内容
【题目】从参加某次高中英语竞赛的学生中抽出100名,将其成绩整理后,绘制频率分布直方图(如图所示).其中样本数据分组区间为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
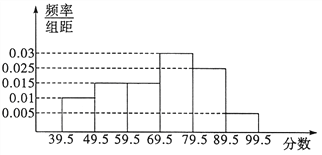
(Ⅰ)试求图中![]() 的值,并计算区间
的值,并计算区间![]() 上的样本数据的频率和频数;
上的样本数据的频率和频数;
(Ⅱ)试估计这次英语竞赛成绩的众数、中位数及平均成绩(结果精确到![]() ).
).
注:同一组数据用该组区间的中点值作为代表
【答案】(Ⅰ)70;(Ⅱ)70.5.
【解析】试题分析:(Ⅰ)根据频率和为1,即矩形面积和为1可得![]() ,所以区间
,所以区间![]() 上的样本数据的频率为
上的样本数据的频率为![]() ,频数为
,频数为![]() . (Ⅱ)
. (Ⅱ)
根据样本的频率分布直方图,众数在![]() 的中点处,熟记中位数平均数的公式求出中位数和平均数
的中点处,熟记中位数平均数的公式求出中位数和平均数
试题解析:
(Ⅰ)由图可知,
![]() ,
, ![]() .
.
区间![]() 上的样本数据的频率为
上的样本数据的频率为
![]() .
.
频数为![]() .
.
(Ⅱ))∵频率最高的是![]() ,估计众数为
,估计众数为![]() ,而中位数是把频率分布直方图分成两个面积相等部分的平行于Y轴的直线横坐标,出现在
,而中位数是把频率分布直方图分成两个面积相等部分的平行于Y轴的直线横坐标,出现在![]() 内,设为
内,设为![]() 所以中位数为
所以中位数为![]() .
.
平均成绩为:
![]()
(结果精确到0.1)

练习册系列答案
相关题目
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.