题目内容
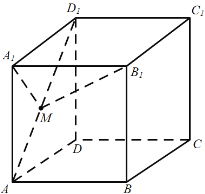
【题目】如图,点![]() 是正方体
是正方体![]() 中的侧面
中的侧面![]() 上的一个动点,则下列结论正确的是( )
上的一个动点,则下列结论正确的是( )
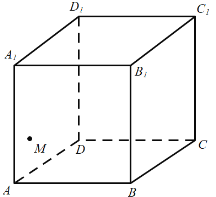
A.点![]() 存在无数个位置满足
存在无数个位置满足![]()
B.若正方体的棱长为1,三棱锥![]() 的体积最大值为
的体积最大值为![]()
C.在线段![]() 上存在点
上存在点![]() ,使异面直线
,使异面直线![]() 与
与![]() 所成的角是
所成的角是![]()
D.点![]() 存在无数个位置满足到直线
存在无数个位置满足到直线![]() 和直线
和直线![]() 的距离相等.
的距离相等.
【答案】ABD
【解析】
通过证明![]() 面
面![]() ,可得当点
,可得当点![]() 上时,有
上时,有![]() ,可判断A;由已知
,可判断A;由已知![]() ,当点
,当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 到面
到面![]() 的距离最大,计算
的距离最大,计算![]() 可判断B;C. 连接
可判断B;C. 连接![]() ,因为
,因为![]() ,则
,则![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角,利用余弦定理算出
所成的角,利用余弦定理算出![]() 的距离,可判断C;连接
的距离,可判断C;连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,得到
,得到![]() ,则点
,则点![]() 在以
在以![]() 为焦点,以
为焦点,以![]() 为准线的抛物线上,可判断D.
为准线的抛物线上,可判断D.
解:A.连接![]() ,
,
由正方体的性质可得![]() ,
,
则![]() 面
面![]()
当点![]() 上时,有
上时,有![]() ,
,
故点![]() 存在无数个位置满足
存在无数个位置满足![]() ,
,
故A正确;
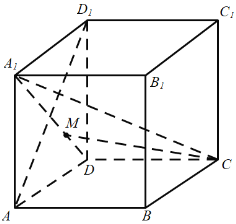
B.由已知![]() ,
,
当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 到面
到面![]() 的距离最大,
的距离最大,
则三棱锥![]() 的体积最大值为
的体积最大值为![]() ,
,
故B正确;
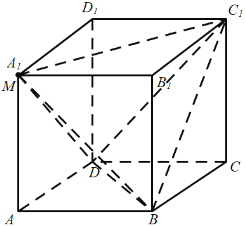
C. 连接![]() ,因为
,因为![]()
则![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角
所成的角
设正方体棱长为1,![]() ,则
,则![]() ,
,
点![]() 到线
到线![]() 的距离为
的距离为![]() ,
,![]()
![]() ,
,
解得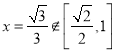 ,
,
所以在线段![]() 上不存在点
上不存在点![]() ,使异面直线
,使异面直线![]() 与
与![]() 所成的角是
所成的角是![]() ,
,
故C错误;
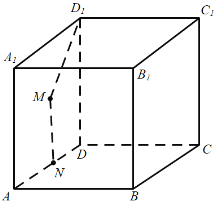
D. 连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
由![]() 面
面![]() ,
,![]() 面
面![]() ,得
,得![]() ,
,
则![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离,![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离,
由已知![]() ,
,
则点![]() 在以
在以![]() 为焦点,以
为焦点,以![]() 为准线的抛物线上,故这样的点
为准线的抛物线上,故这样的点![]() 有无数个,
有无数个,
故D正确.
故选:ABD.

【题目】在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区200名患者的相关信息,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
|
人数 | 17 | 41 | 62 | 50 | 26 | 3 | 1 |
(1)求这200名患者的潜伏期的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述200名患者中抽取40人得到如下列联表.请将列联表补充完整,并根据列联表判断是否有95%的把握认为潜伏期与患者年龄有关;
潜伏期 | 潜伏期 | 总计 | |
50岁以上(含50岁) | 20 | ||
50岁以下 | 9 | ||
总计 | 40 |
(3)以这200名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入硏究,该研究团队在该地区随机调查了10名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
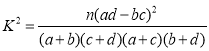 ,其中
,其中![]()