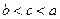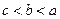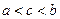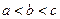题目内容
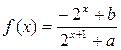
(1)求
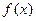 的解析式;
的解析式;(2)若对于实数
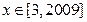 ,不等式
,不等式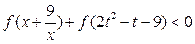 恒成立,求t
恒成立,求t的取值范围.
(1)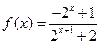 (2)
(2)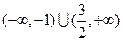
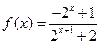 (2)
(2)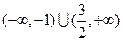
(1)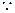
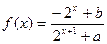 是定义域为
是定义域为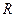 的奇函数,
的奇函数,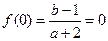 ,即
,即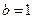
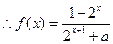 又
又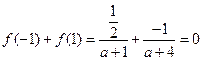 ,
,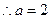
所以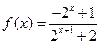 ……5分
……5分
另法:因为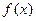 是
是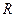 上的奇函数,所以
上的奇函数,所以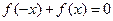
即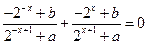
化简得: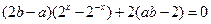
又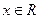 这个等式恒成立,所以
这个等式恒成立,所以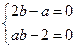 ,即
,即
但当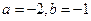 时,
时, ,
,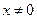 ,即
,即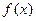 的定义域不是
的定义域不是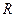 ,所以,
,所以,
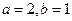 ,
,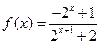 …… 5分
…… 5分
(2)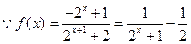
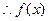 在
在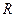 上是减函数(证明略)。 … 6分
上是减函数(证明略)。 … 6分
又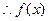 是奇函数,由
是奇函数,由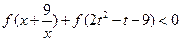 得
得
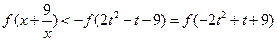 ……9分
……9分
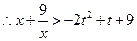
这个不等式对于实数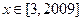 恒成立 ……11分
恒成立 ……11分
因为函数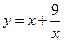 在区间
在区间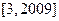 上是增函数,所以当
上是增函数,所以当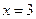 时
时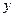 最小
最小 ,从而
,从而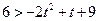 ,即
,即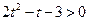 所以,
所以,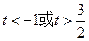
故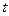 的取值范围是
的取值范围是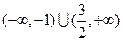 。 …… 14分
。 …… 14分
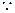
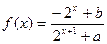 是定义域为
是定义域为 的奇函数,
的奇函数,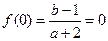 ,即
,即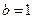
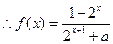 又
又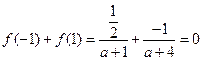 ,
,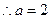
所以
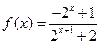 ……5分
……5分另法:因为
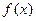 是
是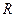 上的奇函数,所以
上的奇函数,所以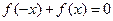
即
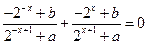
化简得:
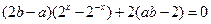
又
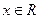 这个等式恒成立,所以
这个等式恒成立,所以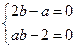 ,即
,即
但当
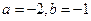 时,
时, ,
,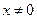 ,即
,即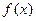 的定义域不是
的定义域不是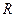 ,所以,
,所以,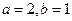 ,
,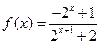 …… 5分
…… 5分(2)
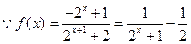
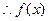 在
在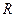 上是减函数(证明略)。 … 6分
上是减函数(证明略)。 … 6分又
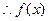 是奇函数,由
是奇函数,由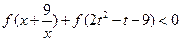 得
得 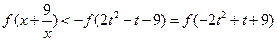 ……9分
……9分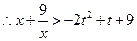
这个不等式对于实数
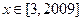 恒成立 ……11分
恒成立 ……11分因为函数
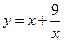 在区间
在区间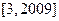 上是增函数,所以当
上是增函数,所以当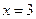 时
时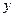 最小
最小 ,从而
,从而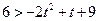 ,即
,即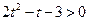 所以,
所以,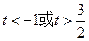
故
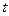 的取值范围是
的取值范围是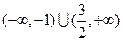 。 …… 14分
。 …… 14分
练习册系列答案
相关题目
 x,求使f(x)=-
x,求使f(x)=-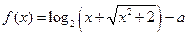 为奇函数,同时使函数
为奇函数,同时使函数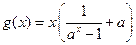 为偶函数,证明你的结论。
为偶函数,证明你的结论。 上的函数
上的函数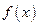 为偶函数,则
为偶函数,则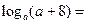 .
. 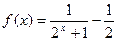 。(1)判断函数
。(1)判断函数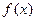 的奇偶性;
的奇偶性;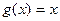
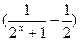 ,求证:对于任意
,求证:对于任意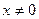 ,都有
,都有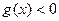 。
。 ]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。
]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。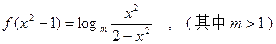
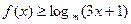
 是偶函数,而
是偶函数,而 是奇函数,且对任意
是奇函数,且对任意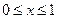 ,都有
,都有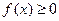 ,则
,则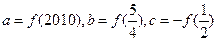 的大小关系是( )
的大小关系是( )