题目内容
已知函数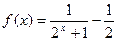 。(1)判断函数
。(1)判断函数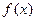 的奇偶性;
的奇偶性;
(2)设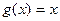
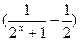 ,求证:对于任意
,求证:对于任意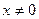 ,都有
,都有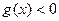 。
。
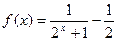 。(1)判断函数
。(1)判断函数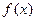 的奇偶性;
的奇偶性;(2)设
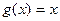
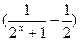 ,求证:对于任意
,求证:对于任意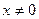 ,都有
,都有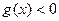 。
。(1)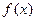 为奇函数
为奇函数
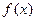 为奇函数
为奇函数(1)易知,函数定义域为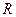 ,且
,且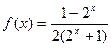 1分
1分
由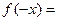
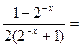
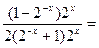
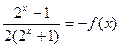 4分
4分
故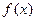 为奇函数。 5分
为奇函数。 5分
(2) 当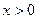 时,
时,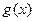
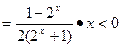 ; 7分
; 7分
易知,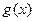 为偶函数。 8分
为偶函数。 8分
故当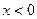 时,
时,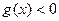 。 9分
。 9分
因此,对于任意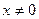 ,都有
,都有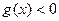 。 10分
。 10分
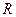 ,且
,且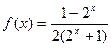 1分
1分由
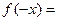
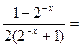
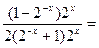
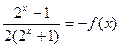 4分
4分 故
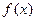 为奇函数。 5分
为奇函数。 5分(2) 当
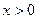 时,
时,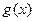
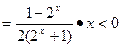 ; 7分
; 7分易知,
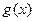 为偶函数。 8分
为偶函数。 8分 故当
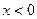 时,
时,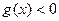 。 9分
。 9分因此,对于任意
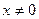 ,都有
,都有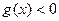 。 10分
。 10分 
练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
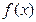 是定义在R上的偶函数,其图象关于直线
是定义在R上的偶函数,其图象关于直线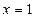 对称,证明
对称,证明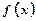 、
、 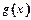 都是偶函数,则
都是偶函数,则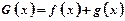 是【 】.
是【 】. 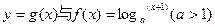 的图象关于原点对称.
的图象关于原点对称.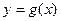 的解析式;
的解析式;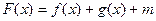 为奇函数,试确定实数m的值;
为奇函数,试确定实数m的值;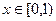 时,总有
时,总有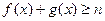 成立,求实数n的取值范围.
成立,求实数n的取值范围.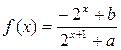
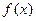 的解析式;
的解析式;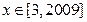 ,不等式
,不等式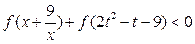 恒成立,求t
恒成立,求t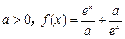 是
是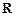 上的偶函数,求
上的偶函数,求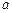 的值.
的值.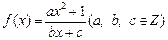 是奇函数,又,
是奇函数,又,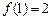 ,
,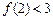 ,
,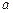 、
、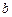 、
、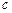 的值.
的值.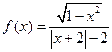 (2)
(2)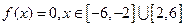
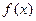 是定义在区间
是定义在区间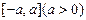 上的奇函数,若
上的奇函数,若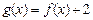 ,则
,则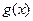 的最大值与最小值之和为 .
的最大值与最小值之和为 .