Question

【题目】已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜ ）的部分图象如图所示，下列说法正确的是（ ）
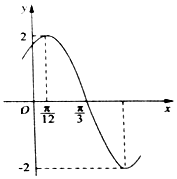
A.函数f（x）的图象关于直线x=﹣ 对称
B.函数f（x）的图象关于点（﹣ ，0）对称
C.若方程f（x）=m在[﹣ ，0]上有两个不相等的实数根，则实数m∈（﹣2，﹣ ]
D.将函数f（x）的图象向左平移 个单位可得到一个偶函数

Answer 1

【答案】C
【解析】解：根据函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜ ）的部分图象，可得A=2， = ﹣ ，∴ω=2． 再根据五点法作图，可得2 +φ=π，∴φ= ，f（x）=2sin（2x+ ）．
当x=﹣ 时，f（x）=0，不是最值，故函数f（x）的图象不关于直线x=﹣ 对称，故排除A；
当x=﹣ 时，f（x）=﹣2，是最值，故函数f（x）的图象关于直线x=﹣ 对称，故排除B；
在[﹣ ，0]上，2x+ ∈[﹣ ， ]，方程f（x）=m在[﹣ ，0]上有两个不相等的实数根，则实数m∈（﹣2，﹣ ]，故C正确；
将函数f（x）的图象向左平移 个单位，可得y=2sin（2x+ + ）=﹣sin2x 的图象，故所得函数为奇函数，故排除D，
故选：C．
由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值，可得f（x）的解析式；再利用正弦函数的定义域和值域，正弦函数的图象和性质，判断各个选项是否正确，从而得出结论．