题目内容
【题目】已知![]() ,设
,设![]() 成立;
成立; ![]() 成立. 如果“
成立. 如果“![]() ”为真,“
”为真,“![]() ”为假,求实数
”为假,求实数![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】试题分析:若命题p为真,通过分离参变量求出函数![]() ,在
,在![]() 时的最小值,可得m的取值范围;若命题q为真,则
时的最小值,可得m的取值范围;若命题q为真,则![]() 在
在![]() 有解,构造函数
有解,构造函数![]() ,求出函数的最大值,可得m的取值范围; “
,求出函数的最大值,可得m的取值范围; “![]() ”为真,“
”为真,“![]() ”为假,即
”为假,即![]() 与
与![]() 一真一假,分类讨论解出m的范围.
一真一假,分类讨论解出m的范围.
试题解析:
若![]() 为真,则对
为真,则对![]() 恒成立. 设
恒成立. 设![]() ,
,
配方得![]() ,∴
,∴![]() 在
在![]() 上的最小值为-3,∴
上的最小值为-3,∴![]() 解得
解得![]() ,
,
∴![]() 为真时,
为真时, ![]() .若
.若![]() 为真,则
为真,则![]() 成立,即
成立,即![]() 成立.
成立.
设![]() ,则
,则![]() 在
在![]() 上是增函数,∴
上是增函数,∴![]() 的最大值为
的最大值为![]() ,
,
∴![]() ∴
∴![]() 为真时,
为真时, ![]() ∵“
∵“![]() ”为真,“
”为真,“![]() ”为假,∴
”为假,∴![]() 与
与![]() 一真一假.
一真一假.
当![]() 真
真![]() 假时,
假时, 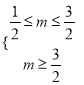 ,∴
,∴![]()
当![]() 假
假![]() 真时,
真时, 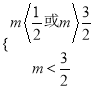 ∴
∴![]()
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
点睛: 本题考查全特称命题的真假判断以及通过恒成立有解问题转化的函数最值问题.对全称(存在性)命题进行否定的两步操作:①找到命题所含的量词,没有量词的要结合命题的含义加上量词,再进行否定;②对原命题的结论进行否定.判定全称命题“![]() x∈M,p(x)”是真命题,需要对集合M中的每个元素x,证明p(x)成立;要判定一个全称命题是假命题,只要举出集合M中的一个特殊值x0,使p(x0)不成立即可.要判断存在性命题是真命题,只要在限定集合内至少能找到一个x=x0,使p(x0)成立即可,否则就是假命题.
x∈M,p(x)”是真命题,需要对集合M中的每个元素x,证明p(x)成立;要判定一个全称命题是假命题,只要举出集合M中的一个特殊值x0,使p(x0)不成立即可.要判断存在性命题是真命题,只要在限定集合内至少能找到一个x=x0,使p(x0)成立即可,否则就是假命题.

练习册系列答案
相关题目