题目内容
1.已知任意一个正整数的三次幂可表示成一些连续奇数的和,如图所示,33可表示为7+9+11,则我们把7、9、11叫做它的“数因子”,若n3的一个“数因子”为2015,则n=45.13=1
23=2+5
33=7+9+11
43=13+15+17+19
…
分析 由题意和等差数列的前n项和公式,求出前n个正整数的三次幂的“数因子”的个数是$\frac{n(n+1)}{2}$,再判断出2015是第1008个奇数,再由条件和特值法判断出2015应是453的一个“数因子”.
解答 解:由题意知,n3可表示为n个连续奇数的和,且所有正整数的“数因子”都是按照从小到大的顺序排列的,
所以前n个正整数的三次幂的“数因子”共有1+2+3+…+n=$\frac{n(n+1)}{2}$个,
因为2015=2×1008-1,故2015是第1008个奇数,
而$\frac{44×45}{2}$=990<1008,$\frac{45×46}{2}$=1035>1008,
所以443的最大“数因子”是第990个奇数,
453的最大“数因子”是第1035个奇数,
故第1008个奇数:2015应是453的一个“数因子”,
故答案为:45
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知An2=132,则n=( )
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
9.曲线y=ax在x=0点处的切线方程是xln2+y-1=0,则a=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | ln2 | D. | ln$\frac{1}{2}$ |
16.已知全集I={-1,-2,-3,0,1},M={-1,0,a2+1},则∁IM为( )
| A. | {-1,-2,-3,1} | B. | {-1,0,1} | C. | {-1,-3} | D. | {-2,-3} |
13.过点M(1,2),N(m,3)的直线与2x-3y+1=0垂直,则m的值为( )
| A. | 1 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | -1 |
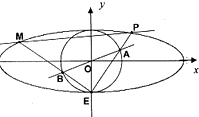 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=b2,已知椭圆C1过点(1,$\frac{\sqrt{2}}{2}$),焦距为2.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=b2,已知椭圆C1过点(1,$\frac{\sqrt{2}}{2}$),焦距为2.