Question

【题目】在直角坐标系xOy中，直线l的参数方程为 （t为参数），在以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，曲线C的极坐标方程为ρ=2 cos（ +θ）．
（I）求直线l的普通方程和曲线C的直角坐标方程；
（Ⅱ）设直线l与曲线C相交于M，N两点，求|MN|的值．

Answer 1

【答案】解：（Ⅰ）∵直线l的参数方程为 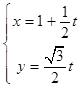（t为参数），

∴消去参数t，得直线l的直角坐标方程为 =0．

∵曲线C的极坐标方程为ρ=2 cos（ +θ）．

即 =2cosθ﹣2sinθ，

即ρ2=2ρcosθ﹣2ρsinθ，

∴曲线C的直角坐标方程为x2+y2=2x﹣2y，即（x﹣1）2+（y+1）2=2．

（Ⅱ）曲线C是以C（1，﹣1）为圆心，以r= 为半径的圆，

圆心C（1，﹣1）到直线l的距离d= = ，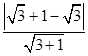

∵直线l与曲线C相交于M，N两点，

∴|MN|=2 =2 =

【解析】（Ⅰ）直线l的参数方程消去参数t，得直线l的直角坐标方程为 =0；曲线C的极坐标方程l转化为ρ2=2ρcosθ﹣2ρsinθ，由此能求出曲线C的直角坐标方程．（Ⅱ）曲线C是以C（1，﹣1）为圆心，以r= 为半径的圆，求出圆心C（1，﹣1）到直线l的距离d，由|MN|=2 ，能求出结果．