题目内容
(本小题满分12分)
数列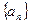 的各项均为正数,
的各项均为正数,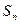 为其前
为其前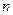 项和,对于任意
项和,对于任意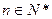 ,总有
,总有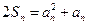 .
.
(1) 求数列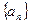 的通项公式;
的通项公式;
(2) 设正数数列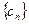 满足
满足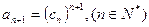 ,求数列
,求数列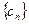 中的最大项;
中的最大项;
数列
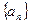 的各项均为正数,
的各项均为正数,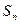 为其前
为其前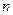 项和,对于任意
项和,对于任意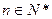 ,总有
,总有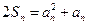 .
.(1) 求数列
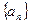 的通项公式;
的通项公式;(2) 设正数数列
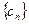 满足
满足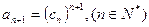 ,求数列
,求数列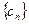 中的最大项;
中的最大项;(1) 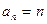
(2) 数列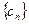 中的最大项为
中的最大项为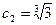
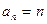
(2) 数列
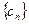 中的最大项为
中的最大项为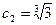
解:(1)由已知:对于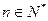 ,总有
,总有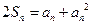 ①成立
①成立
∴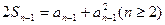 ②
②
①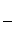 ②得
②得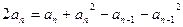
∴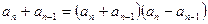 ∵
∵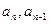 均为正数,∴
均为正数,∴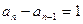
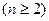
∴数列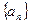 是公差为1的等差数列 又
是公差为1的等差数列 又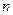 =1时,
=1时,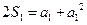 , 解得
, 解得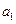 =1.
=1.
∴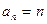 . ………………………………………6分
. ………………………………………6分
(2)(解法一)由已知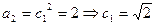 ,
,
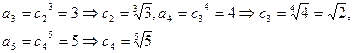
易得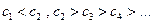 猜想
猜想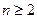 时,
时,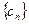 是递减数列............8分
是递减数列............8分
令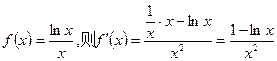
∵当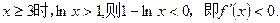
∴在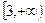 内
内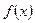 为单调递减函数.....................................10分
为单调递减函数.....................................10分
由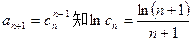 .
.
∴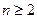 时,
时, 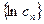 是递减数列.即
是递减数列.即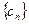 是递减数列.
是递减数列.
又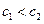 , ∴数列
, ∴数列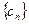 中的最大项为
中的最大项为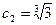 . ………………………………12分
. ………………………………12分
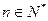 ,总有
,总有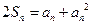 ①成立
①成立∴
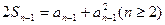 ②
② ①
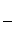 ②得
②得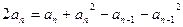
∴
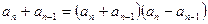 ∵
∵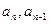 均为正数,∴
均为正数,∴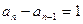
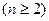
∴数列
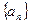 是公差为1的等差数列 又
是公差为1的等差数列 又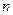 =1时,
=1时,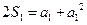 , 解得
, 解得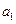 =1.
=1.∴
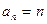 . ………………………………………6分
. ………………………………………6分 (2)(解法一)由已知
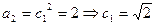 ,
, 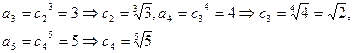
易得
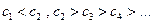 猜想
猜想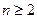 时,
时,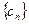 是递减数列............8分
是递减数列............8分 令
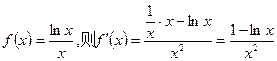
∵当
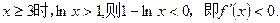
∴在
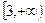 内
内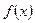 为单调递减函数.....................................10分
为单调递减函数.....................................10分由
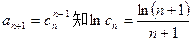 .
.∴
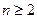 时,
时, 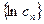 是递减数列.即
是递减数列.即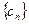 是递减数列.
是递减数列.又
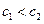 , ∴数列
, ∴数列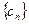 中的最大项为
中的最大项为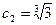 . ………………………………12分
. ………………………………12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
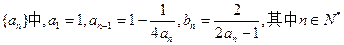 。
。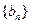 是等差数列,并求数列
是等差数列,并求数列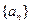 的通项公式;
的通项公式;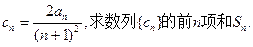
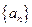 的前
的前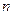 项和
项和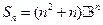 .
.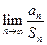 ; (Ⅱ)证明:
; (Ⅱ)证明: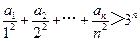 .
. 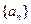 的前
的前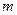 项和为20,前
项和为20,前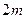 项和为70,则它的前
项和为70,则它的前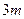 的和为( )
的和为( )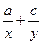 的值为( )
的值为( )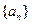 中,
中,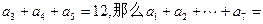 ( )
( ) 的前n项和为
的前n项和为 ,且
,且 ,则公差
,则公差
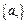 中,若
中,若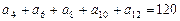 ,则
,则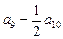 的值为:
的值为: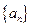 的通项公式为
的通项公式为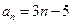 ,则
,则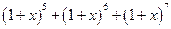 的展开式中含
的展开式中含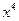 项的系数是该数列的
项的系数是该数列的  ( )
( )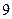 项
项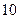 项
项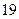 项
项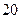 项
项