题目内容
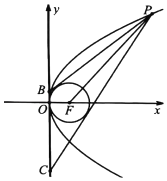
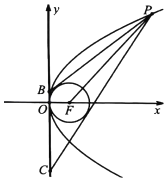
【题目】如图,P是抛物线E:y2=4x上的动点,F是抛物线E的焦点.
(1)求|PF|的最小值;
(2)点B,C在y轴上,直线PB,PC与圆(x﹣1)2+y2=1相切.当|PF|∈[4,6]时,求|BC|的最小值.
【答案】(1)|PF|的最小值为1(2)![]()
【解析】
(1)求得抛物线的焦点和准线方程,运用抛物线的定义和性质,即可求得|PF|的最小值;
(2)设![]() ,分别求得
,分别求得![]() 的方程,运用直线和圆相切,得到
的方程,运用直线和圆相切,得到![]() 为方程
为方程![]() 的两根,再由韦达定理可得
的两根,再由韦达定理可得![]() ,进而可求得其最小值.
,进而可求得其最小值.
(1)P是抛物线E:y2=4x上的动点,F是抛物线E的焦点(1,0),准线方程为x=﹣1,
由抛物线的定义可得|PF|=d=xP+1,
由![]() ,可得d的最小值为1,|PF|的最小值为1;
,可得d的最小值为1,|PF|的最小值为1;
(2)设![]() ,
,
则PB的方程为y![]() x+m,PC的方程为y
x+m,PC的方程为y![]() x+n,
x+n,
由直线PA与圆(x﹣1)2+y2=1相切,可得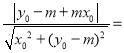 1,
1,
整理得(x0﹣2)m2+2y0m﹣x0=0,
同理可得(x0﹣2)n2+2y0n﹣x0=0,
即有m,n为方程(x0﹣2)x2+2y0x﹣x0=0的两根,可得m+n![]() ,mn
,mn![]() ,
,
则|m﹣n|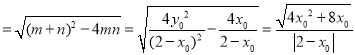 ,
,
由|PF|∈[4,6],可得x0+1∈[4,6],即x0∈[3,5],
令t=|2﹣x0|=x0﹣2,t∈[1,3],
即有|m﹣n|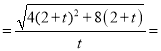 2
2![]() 在[1,3]递减,
在[1,3]递减,
可得t=3即x0=5时,|BC|=|m﹣n|取得最小值![]() .
.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】某水果种植基地引进一种新水果品种,经研究发现该水果每株的产量![]() (单位:
(单位:![]() )和与它“相近”的株数
)和与它“相近”的株数![]() 具有线性相关关系(两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出该种水果每株的产量![]() 关于它“相近”株数
关于它“相近”株数![]() 的回归方程;
的回归方程;
(2)有一种植户准备种植该种水果500株,且每株与它“相近”的株数都为![]() ,计划收获后能全部售出,价格为10元
,计划收获后能全部售出,价格为10元![]() ,如果收入(收入=产量×价格)不低于25000元,则
,如果收入(收入=产量×价格)不低于25000元,则![]() 的最大值是多少?
的最大值是多少?
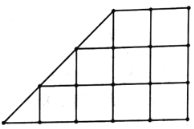
(3)该种植基地在如图所示的直角梯形地块的每个交叉点(直线的交点)处都种了一株该种水果,其中每个小正方形的边长和直角三角形的直角边长都为![]() ,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: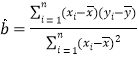 ,
,![]() .
.
【题目】学校为了解高二学生每天自主学习中国古典文学的时间,随机抽取了高二男生和女生各50名进行问卷调查,其中每天自主学习中国古典文学的时间超过3小时的学生称为“古文迷”,否则为“非古文迷”,调查结果如下表:
古文迷 | 非古文迷 | 合计 | |
男生 | 26 | 24 | 50 |
女生 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
参考公式: ,其中
,其中![]()
参考数据:
| 0.500 | 0.400 | 0.250 | 0.050 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
(1)根据上表数据判断能否有60%的把握认为“古文迷”与性别有关?
(2)现从调查的女生中按分层抽样的方法抽出5人进行理科学习时间的调查,求所抽取的5人中“古文迷”和“非古文迷”的人数;