题目内容
11. 如图,在三棱锥A-BCD中,△ACD与△BCD是全等的等腰三角形,且平面ACD⊥平面BCD,AB=2CD=4,则该三棱锥的外接球的表面积为$\frac{65}{4}π$.
如图,在三棱锥A-BCD中,△ACD与△BCD是全等的等腰三角形,且平面ACD⊥平面BCD,AB=2CD=4,则该三棱锥的外接球的表面积为$\frac{65}{4}π$.
分析 取AB,CD中点分别为E,F,连接EF,AF,BF,求出EF,判断三棱锥的外接球球心O在线段EF上,连接OA,OC,求出半径,然后求解表面积.
解答 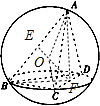 解:取AB,CD中点分别为E,F,连接EF,AF,BF,由题意知AF⊥BF,AF=BF,EF=2,易知三棱锥的外接球球心O在线段EF上,连接OA,OC,有R2=AE2+OE2,R2=CF2+OF2,求得${R^2}=\frac{65}{16}$,所以其表面积为$\frac{65}{4}π$.
解:取AB,CD中点分别为E,F,连接EF,AF,BF,由题意知AF⊥BF,AF=BF,EF=2,易知三棱锥的外接球球心O在线段EF上,连接OA,OC,有R2=AE2+OE2,R2=CF2+OF2,求得${R^2}=\frac{65}{16}$,所以其表面积为$\frac{65}{4}π$.
故答案为:$\frac{65}{4}π$.
点评 本小题主要考查球的内接几何体的相关计算问题,对考生的空间想象能力与运算求解能力以及数形结合思想都提出很高要求,本题是一道综合题,属于较难题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
19.已知F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两个焦点,P是C上一点,若|PF1|•|PF2|=8a2,且△PF1F2的最小内角为30°,则双曲线C的离心率是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
6.如图是一个几何体的三视图,则这个几何体的体积为( )


| A. | 16+3π | B. | 32+6π | C. | 64+12π | D. | 64+6π |
1.棱长均为4的三棱锥的顶点都在同一个球面上,则该球的表面积为( )
| A. | $\frac{8}{3}π$ | B. | 6π | C. | 16π | D. | 24π |
 十八世纪,法国数学家布丰和勒可莱尔提出投针问题:在平面上画有一组间距为a的平行线,将一根长度为l的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率p=$\frac{2l}{πa}$(π为圆周率).已知l=3.14,a=6,π≈3.14,现随机掷14根相同的针(长度为l)在这个平面上,记这些针与平行线(间距为a)相交的根数为m,其相应的概率为p(m).当p(m)取得最大值时,m=4或5.
十八世纪,法国数学家布丰和勒可莱尔提出投针问题:在平面上画有一组间距为a的平行线,将一根长度为l的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率p=$\frac{2l}{πa}$(π为圆周率).已知l=3.14,a=6,π≈3.14,现随机掷14根相同的针(长度为l)在这个平面上,记这些针与平行线(间距为a)相交的根数为m,其相应的概率为p(m).当p(m)取得最大值时,m=4或5.