题目内容
19.已知F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两个焦点,P是C上一点,若|PF1|•|PF2|=8a2,且△PF1F2的最小内角为30°,则双曲线C的离心率是( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
分析 不妨设点P在双曲线右支,F1,F2分别为左,右焦点,有|PF1|-|PF2|=2a,由条件可得△PF1F2的三边,判断最小的边,从而判断三角形的形状,结合离心率公式计算即可得到.
解答 解:不妨设点P在双曲线右支,F1,F2分别为左,右焦点,
有|PF1|-|PF2|=2a,
由$|P{F_1}|•|P{F_2}|=8{a^2}$,可得|PF1|=4a,|PF2|=2a,
由|F1F2|=2c>2a知,△PF1F2的最小内角为∠PF1F2=30°,
从而△PF1F2为直角三角形,∠F1F2P=90°,
则有2c=2$\sqrt{3}$a,
此时双曲线离心率e=$\frac{c}{a}$=$\sqrt{3}$,
故选C.
点评 本题主要考查双曲线的定义,双曲线离心率的运算,对考生的运算求解能力提出较高要求.

练习册系列答案
相关题目
14.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x-y-7≥0}\\{x+y-8≥0}\\{x-2y-2≤0}\end{array}\right.$,则目标函数z=x2+y2的最小值为( )
| A. | 32 | B. | 17 | C. | 40 | D. | 34 |
4.在△ABC中,角A,B,C的对边分别是a,b,c,若a2-b2=$\sqrt{3}$bc,sinC=2$\sqrt{3}$sinB,则A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
8.已知a,b是空间中两不同直线,α,β是空间中两不同平面,下列命题中正确的是( )
| A. | 若直线a∥b,b?α,则a∥α | B. | 若平面α⊥β,a⊥α,则a∥β | ||
| C. | 若平面α∥β,a?α,b?β,则a∥b | D. | 若a⊥α,b⊥β,a∥b,则α∥β |
9.执行如图所示的程序框图,输出的结果为( )
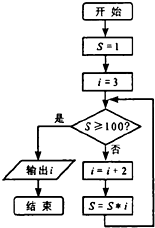

| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
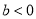 ,且
,且 ,则
,则 等于( )
等于( )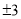 B.-2
B.-2 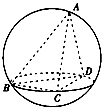 如图,在三棱锥A-BCD中,△ACD与△BCD是全等的等腰三角形,且平面ACD⊥平面BCD,AB=2CD=4,则该三棱锥的外接球的表面积为$\frac{65}{4}π$.
如图,在三棱锥A-BCD中,△ACD与△BCD是全等的等腰三角形,且平面ACD⊥平面BCD,AB=2CD=4,则该三棱锥的外接球的表面积为$\frac{65}{4}π$.