题目内容
(2013•浙江)在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(Ⅰ)求d,an;
(Ⅱ)若d<0,求|a1|+|a2|+|a3|+…+|an|.
(Ⅰ)求d,an;
(Ⅱ)若d<0,求|a1|+|a2|+|a3|+…+|an|.
(1)d=﹣1或d=4;an=﹣n+11或an=4n+6
(2)|a1|+|a2|+|a3|+…+|an|=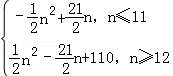 .
.
(2)|a1|+|a2|+|a3|+…+|an|=
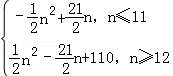 .
.(Ⅰ)由题意得 ,即
,即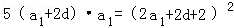 ,整理得d2﹣3d﹣4=0.解得d=﹣1或d=4.
,整理得d2﹣3d﹣4=0.解得d=﹣1或d=4.
当d=﹣1时,an=a1+(n﹣1)d=10﹣(n﹣1)=﹣n+11.
当d=4时,an=a1+(n﹣1)d=10+4(n﹣1)=4n+6.
所以an=﹣n+11或an=4n+6;
(Ⅱ)设数列{an}的前n项和为Sn,因为d<0,由(Ⅰ)得d=﹣1,an=﹣n+11.
则当n≤11时,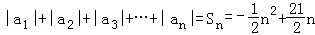 .
.
当n≥12时,|a1|+|a2|+|a3|+…+|an|=﹣Sn+2S11=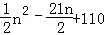 .
.
综上所述,
|a1|+|a2|+|a3|+…+|an|=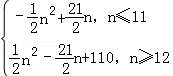 .
.
 ,即
,即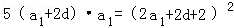 ,整理得d2﹣3d﹣4=0.解得d=﹣1或d=4.
,整理得d2﹣3d﹣4=0.解得d=﹣1或d=4.当d=﹣1时,an=a1+(n﹣1)d=10﹣(n﹣1)=﹣n+11.
当d=4时,an=a1+(n﹣1)d=10+4(n﹣1)=4n+6.
所以an=﹣n+11或an=4n+6;
(Ⅱ)设数列{an}的前n项和为Sn,因为d<0,由(Ⅰ)得d=﹣1,an=﹣n+11.
则当n≤11时,
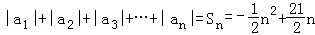 .
.当n≥12时,|a1|+|a2|+|a3|+…+|an|=﹣Sn+2S11=
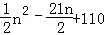 .
.综上所述,
|a1|+|a2|+|a3|+…+|an|=
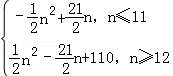 .
.
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目

 ,数列{bn}的前n项和为Tn.证明:对于任意n
,数列{bn}的前n项和为Tn.证明:对于任意n  N*,都有Tn<
N*,都有Tn<
 按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一
按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一 构成公差为
构成公差为 的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为
的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为 的等比数列.若
的等比数列.若 ,
, ,
, .
.
 的值;
的值; 行各数的和
行各数的和 .
. 是一个等差数列且
是一个等差数列且 ,
, ,
, 项和
项和 的最小值.
的最小值. 天,为使投资的回报最多,你会选择哪种方案投资?( )
天,为使投资的回报最多,你会选择哪种方案投资?( ) ).若数列{
).若数列{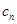 }的前
}的前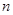 项和为
项和为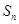 ,则
,则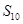 = (用数字作答).
= (用数字作答). 


