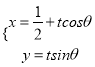题目内容
【题目】如图,某市建有贯穿东西和南北的两条垂直公路![]() ,
,![]() ,在它们交叉路口点
,在它们交叉路口点![]() 处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台
处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台![]() 位于两条垂直公路的角平分线
位于两条垂直公路的角平分线![]() 上,
上,![]() 与环形公路的交点记作
与环形公路的交点记作![]() .游客游览荷花池时,需沿公路
.游客游览荷花池时,需沿公路![]() 先到达环形公路
先到达环形公路![]() 处.为了分流游客,方便游客游览荷花池,计划从靠近公路
处.为了分流游客,方便游客游览荷花池,计划从靠近公路![]() ,
,![]() 的环形公路上选
的环形公路上选![]() ,
,![]() 两处(
两处(![]() ,
,![]() 关于直线
关于直线![]() 对称)修建直达观景台
对称)修建直达观景台![]() 的玻璃栈道
的玻璃栈道![]() ,
,![]() .以
.以![]() ,
,![]() 所在的直线为
所在的直线为![]() ,
,![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() ,靠近公路
,靠近公路![]() ,
,![]() 的环形公路可用曲线
的环形公路可用曲线![]() 近似表示,曲线
近似表示,曲线![]() 符合函数
符合函数![]() .
.
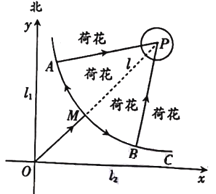
(1)若![]() 百米,点
百米,点![]() 到
到![]() 的垂直距离为1百米,求玻璃栈道
的垂直距离为1百米,求玻璃栈道![]() 的总长度;
的总长度;
(2)若要使得玻璃栈道![]() 的总长度最小为
的总长度最小为![]() 百米,求观景台
百米,求观景台![]() 的位置.
的位置.
【答案】(1)![]() 百米.(2)
百米.(2)![]()
【解析】
(1)由![]() 百米可得
百米可得![]() ,点
,点![]() 到
到![]() 的垂直距离为1百米可得
的垂直距离为1百米可得![]() ,用平面两点间的距离公式可求解答案.
,用平面两点间的距离公式可求解答案.
(2)根据题意即![]() 的最小值为
的最小值为![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,然后换元求出最值,解出
,然后换元求出最值,解出![]() 的值.
的值.
解:(1)在平面直角坐标系![]() 中,设定点
中,设定点![]() ,
,
因为![]() ,所以
,所以![]() ,解得
,解得![]() ,即点
,即点![]() .
.
因为点![]() 到
到![]() 的垂直距离为1百米,所以点
的垂直距离为1百米,所以点![]() ;
;
所以![]() ,
,
又因为![]() ,
,![]() 关于直线
关于直线![]() 对称,点
对称,点![]() 在直线
在直线![]() 上,
上,
所以![]() .即
.即![]() .
.
所以玻璃栈道![]() 的总长度是
的总长度是![]() 百米.
百米.
(2)在平面直角坐标系![]() 中,
中,![]() ,设定点
,设定点![]() ,
,
动点![]() ,因为
,因为![]() ,
,![]() 关于直线
关于直线![]() 对称,
对称,
点![]() 在直线
在直线![]() 上,所以
上,所以![]() .
.
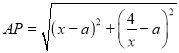 ,则
,则![]() ,
,
令![]() ,则
,则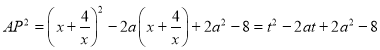 ,
,
函数![]() 的导数
的导数![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调减,所以
上单调减,所以![]()
函数![]() ,
,![]() 图象对称轴是
图象对称轴是![]() ,
,
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,无最小值;
上单调递增,无最小值;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
即![]() 在
在![]() 时有最小值
时有最小值![]() ,
,
由题意![]() ,因为
,因为![]() ,所以
,所以![]() .
.
所以若要使得玻璃栈道![]() 总长度最小为
总长度最小为![]() 百米,观景平台
百米,观景平台![]() 的坐标是
的坐标是![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目