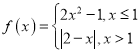题目内容
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,证明:对
时,证明:对![]() ;
;
(2)若函数![]() 在
在![]() 上存在极值,求实数
上存在极值,求实数![]() 的取值范围。
的取值范围。
【答案】(1)见证明;(2) ![]()
【解析】
(1)利用导数说明函数的单调性,进而求得函数的最小值,得到要证明的结论;
(2)问题转化为导函数在区间上有解,法一:对a分类讨论,分别研究a的不同取值下,导函数的单调性及值域,从而得到结论.法二:构造函数,利用函数的导数判断函数的单调性求得函数的值域,再利用零点存在定理说明函数存在极值.
(1)当![]() 时,
时,![]() ,于是,
,于是,![]() .
.
又因为,当![]() 时,
时,![]() 且
且![]() .
.
故当![]() 时,
时,![]() ,即
,即![]() .
.
所以,函数![]() 为
为![]() 上的增函数,于是,
上的增函数,于是,![]() .
.
因此,对![]() ,
,![]() ;
;
(2) 方法一:由题意![]() 在
在![]() 上存在极值,则
上存在极值,则![]() 在
在![]() 上存在零点,
上存在零点,
①当![]() 时,
时,![]() 为
为![]() 上的增函数,
上的增函数,
注意到![]() ,
,![]() ,
,
所以,存在唯一实数![]() ,使得
,使得![]() 成立.
成立.
于是,当![]() 时,
时,![]() ,
,![]() 为
为![]() 上的减函数;
上的减函数;
当![]() 时,
时,![]() ,
,![]() 为
为![]() 上的增函数;
上的增函数;
所以![]() 为函数
为函数![]() 的极小值点;
的极小值点;
②当![]() 时,
时,![]() 在
在![]() 上成立,
上成立,
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 在
在![]() 上没有极值;
上没有极值;
③当![]() 时,
时,![]() 在
在![]() 上成立,
上成立,
所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 在
在![]() 上没有极值,
上没有极值,
综上所述,使![]() 在
在![]() 上存在极值的
上存在极值的![]() 的取值范围是
的取值范围是![]() .
.
方法二:由题意,函数![]() 在
在![]() 上存在极值,则
上存在极值,则![]() 在
在![]() 上存在零点.
上存在零点.
即![]() 在
在![]() 上存在零点.
上存在零点.
设![]() ,
,![]() ,则由单调性的性质可得
,则由单调性的性质可得![]() 为
为![]() 上的减函数.
上的减函数.
即![]() 的值域为
的值域为![]() ,所以,当实数
,所以,当实数![]() 时,
时,![]() 在
在![]() 上存在零点.
上存在零点.
下面证明,当![]() 时,函数
时,函数![]() 在
在![]() 上存在极值.
上存在极值.
事实上,当![]() 时,
时,![]() 为
为![]() 上的增函数,
上的增函数,
注意到![]() ,
,![]() ,所以,存在唯一实数
,所以,存在唯一实数![]() ,
,
使得![]() 成立.于是,当
成立.于是,当![]() 时,
时,![]() ,
,![]() 为
为![]() 上的减函数;
上的减函数;
当![]() 时,
时,![]() ,
,![]() 为
为![]() 上的增函数;
上的增函数;
即![]() 为函数
为函数![]() 的极小值点.
的极小值点.
综上所述,当![]() 时,函数
时,函数![]() 在
在![]() 上存在极值.
上存在极值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】中国武汉于2019年10月18日至2019年10月27日成功举办了第七届世界军人运动会.来自109个国家的9300余名运动员同台竞技.经过激烈的角逐,奖牌榜的前3名如下:
国家 | 金牌 | 银牌 | 铜牌 | 奖牌总数 |
中国 | 133 | 64 | 42 | 239 |
俄罗斯 | 51 | 53 | 57 | 161 |
巴西 | 21 | 31 | 36 | 88 |
某数学爱好者采用分层抽样的方式,从中国和巴西获得金牌选手中抽取了22名获奖代表.从这22名中随机抽取3人, 则这3人中中国选手恰好1人的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()