题目内容
一个酒杯的轴截面是抛物线的一部分,它的方程是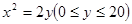 .在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围是( )
.在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围是( )
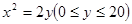 .在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围是( )
.在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围是( ) | A.0<r≤1 | B.0<r<1 | C.0<r≤2 | D.0<r<2 |
A
试题分析:设小球圆心(0,y0),抛物线上点(x,y),求得点到圆心距离平方的表达式,进而根据若r2最小值在(0,0)时取到,则小球触及杯底,需1-y0≥0,进而求得r的范围.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
 在
在 轴右侧,
轴右侧, 的距离减去它到
的距离减去它到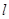 交曲线
交曲线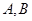 两点,线段
两点,线段 的中点为
的中点为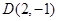 ,求直线
,求直线 上一点
上一点 的纵坐标为4,则点
的纵坐标为4,则点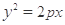 过点
过点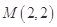 ,则点
,则点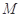 到抛物线焦点的距离为 .
到抛物线焦点的距离为 .