题目内容
设直线l:x-y+m=0与抛物线C:y2=4x交于不同两点A,B,F为抛物线的焦点.
(1)求△ABF的重心G的轨迹方程;
(2)如果m=-2,求△ABF的外接圆的方程.
(1)求△ABF的重心G的轨迹方程;
(2)如果m=-2,求△ABF的外接圆的方程.
(1)y=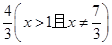 (2)
(2)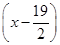 2+
2+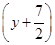 2=
2=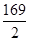
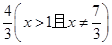 (2)
(2)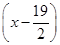 2+
2+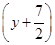 2=
2=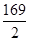
(1)设A(x1,y1),B(x2,y2),F(1,0),重心G(x,y),
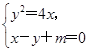 ⇒y2-4y+4m=0,
⇒y2-4y+4m=0,
∴Δ>0⇒m<1且m≠-1(A,B,F不共线),
故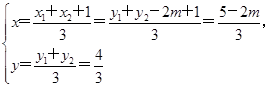
∴重心G的轨迹方程为y=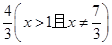 .
.
(2)若m=-2,则y2-4y-8=0,设AB中点为(x0,y0,)
∴y0=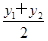 =2,∴x0=y0-m=2-m=4,
=2,∴x0=y0-m=2-m=4,
那么AB的中垂线方程为x+y-6=0,
令△ABF的外接圆圆心为C(a,6-a),
又|AB|=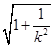 |y1-y2|=4
|y1-y2|=4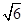 ,C到AB的距离为d=
,C到AB的距离为d=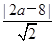 ,∴|CA|=|CF|⇒(2
,∴|CA|=|CF|⇒(2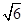 )2+
)2+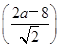 2=(a-1)2+(6-a)2⇒a=
2=(a-1)2+(6-a)2⇒a=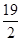 ,
,
∴C点的坐标为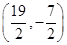 ,∴|CF|2=
,∴|CF|2=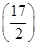 2+
2+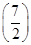 2=
2=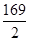 ,
,
∴所求的圆的方程为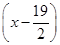 2+
2+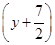 2=
2=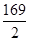 .
.
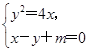 ⇒y2-4y+4m=0,
⇒y2-4y+4m=0,∴Δ>0⇒m<1且m≠-1(A,B,F不共线),
故
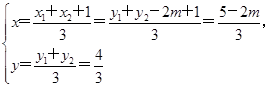
∴重心G的轨迹方程为y=
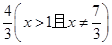 .
.(2)若m=-2,则y2-4y-8=0,设AB中点为(x0,y0,)
∴y0=
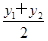 =2,∴x0=y0-m=2-m=4,
=2,∴x0=y0-m=2-m=4,那么AB的中垂线方程为x+y-6=0,
令△ABF的外接圆圆心为C(a,6-a),
又|AB|=
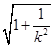 |y1-y2|=4
|y1-y2|=4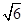 ,C到AB的距离为d=
,C到AB的距离为d=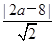 ,∴|CA|=|CF|⇒(2
,∴|CA|=|CF|⇒(2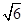 )2+
)2+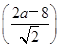 2=(a-1)2+(6-a)2⇒a=
2=(a-1)2+(6-a)2⇒a=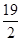 ,
,∴C点的坐标为
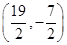 ,∴|CF|2=
,∴|CF|2=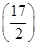 2+
2+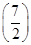 2=
2=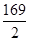 ,
,∴所求的圆的方程为
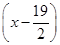 2+
2+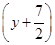 2=
2=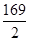 .
.
练习册系列答案
相关题目
 的顶点F是抛物线
的顶点F是抛物线 的焦点,顶点B在抛物线的准线
的焦点,顶点B在抛物线的准线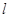 上且
上且 ⊥
⊥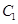 开口内
开口内 值有关
值有关
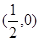

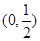
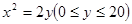 .在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围是( )
.在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围是( ) 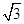 ,那么|PF|=________.
,那么|PF|=________. y,过点A(0,-1)和点B(t,3)的直线与抛物线C没有公共点,则实数t的取值范围是( ).
y,过点A(0,-1)和点B(t,3)的直线与抛物线C没有公共点,则实数t的取值范围是( ). ∪
∪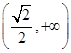
 ∪(2
∪(2 ,+∞)
,+∞) ∪
∪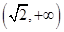
 ,则其标准方程为_______.
,则其标准方程为_______.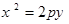
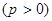 的焦点,M为其上一点,且
的焦点,M为其上一点,且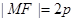 ,则直线MF的斜率为( ).
,则直线MF的斜率为( ).
