题目内容
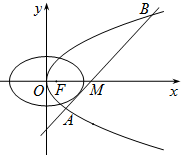
已知过抛物线y2=2px(p>0)的焦点,斜率为2
的直线交抛物线于A(x1,y1)和B(x2,y2)(x1<x2)两点,且|AB|=9,
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若
=
+λ
,求λ的值.
| 2 |
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若
| OC |
| OA |
| OB |
(1)直线AB的方程是y=2
(x-
),与y2=2px联立,有4x2-5px+p2=0,
∴x1+x2=
由抛物线定义得:|AB|=x1+x2+p=9
∴p=4,∴抛物线方程是y2=8x.
(2)由p=4,4x2-5px+p2=0得:x2-5x+4=0,
∴x1=1,x2=4,
y1=-2
,y2=4
,从而A(1,-2
),B(4,4
).
设
=(x3,y3)=(1,-2
)+λ(4,4
)=(4λ+1,4
λ-2
)
又[2
(2λ-1)]2=8(4λ+1),解得:λ=0,或λ=2.
| 2 |
| p |
| 2 |
∴x1+x2=
| 5p |
| 4 |
由抛物线定义得:|AB|=x1+x2+p=9
∴p=4,∴抛物线方程是y2=8x.
(2)由p=4,4x2-5px+p2=0得:x2-5x+4=0,
∴x1=1,x2=4,
y1=-2
| 2 |
| 2 |
| 2 |
| 2 |
设
| OC |
| 2 |
| 2 |
| 2 |
| 2 |
又[2
| 2 |

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
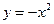 上的点到直线
上的点到直线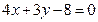 的距离的最小值是 。
的距离的最小值是 。