题目内容
抛物线y2=2px(p>0)上一点M(3,m)到焦点的距离等于5,求抛物线的方程和m的值.
∵抛物线方程为y2=2px
∴抛物线焦点为F(
,0),准线方程为x=-
,
∵点M(3,m)到其焦点的距离为5,
∴p>0,根据抛物线的定义,得3+
=5,
∴p=4,所以抛物线方程为y2=8x
当x=3时,m=±
=±2
.
∴抛物线焦点为F(
| p |
| 2 |
| p |
| 2 |
∵点M(3,m)到其焦点的距离为5,
∴p>0,根据抛物线的定义,得3+
| p |
| 2 |
∴p=4,所以抛物线方程为y2=8x
当x=3时,m=±
| 8×3 |
| 6 |

练习册系列答案
相关题目

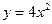 的焦点坐标是 .
的焦点坐标是 .