题目内容
【题目】正方形ABCD一条边AB所在方程为x+3y﹣5=0,另一边CD所在直线方程为x+3y+7=0,
(Ⅰ)求正方形中心G所在的直线方程;
(Ⅱ)设正方形中心G(x0 , y0),当正方形仅有两个顶点在第一象限时,求x0的取值范围.
【答案】解:(Ⅰ)由于正方形中心G所在直线平行于直线x+3y﹣5=0,
设中心所在直线为x+3y+c=0,
由平行线间的距离公式得 ![]() =
= ![]() .
.
解得c=1.
则正方形中心G所在的直线方程为x+3y+1=0;
(Ⅱ)由平行线间的距离公式得正方形的边长为d= ![]() =
= ![]() .
.
设正方形BC,AD所在直线方程为3x﹣y+m=0,
由于中心G(x0 , y0)到BC的距离等于 ![]() =
= ![]() ,
,
那么 ![]() =
= ![]() ,
,
解得m=±6﹣3x0+y0 ①,
又因为G在直线x+3y+1=0上,那么x0+3y0+1=0,即y0=﹣ ![]() ②,
②,
把②代入①得m=±6﹣ ![]() ③,
③,
联立方程 ![]() ,
,
解得 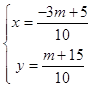 .
.
由于正方形只有两个点在第一象限,那么 ![]() ,
,
就是  ,
,
解得﹣15<m< ![]() ⑤,
⑤,
把③代入⑤得到﹣15<±6﹣ ![]() <
< ![]() ,
,
解得 ![]() <x0<
<x0< ![]() .
.
故x0的取值范围为 ![]()
【解析】(Ⅰ)设中心所在直线为x+3y+c=0,结合正方形的性质和平行线间的距离公式求得c的值;(Ⅱ)由平行线间的距离公式得正方形的边长.设正方形BC,AD所方程为3x﹣y+m=0,联立点G所在直线x0+3y0+1=0,得到 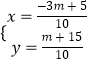 .结合限制性条件正方形仅有两个顶点在第一象限,得到﹣15<m<
.结合限制性条件正方形仅有两个顶点在第一象限,得到﹣15<m< ![]() ,易求x0的取值范围为
,易求x0的取值范围为 ![]() .
.
【考点精析】本题主要考查了两平行线的距离的相关知识点,需要掌握已知两条平行线直线![]() 和
和![]() 的一般式方程为
的一般式方程为![]() :
:![]() ,
,![]()
![]() ,则
,则![]() 与
与![]() 的距离为
的距离为 才能正确解答此题.
才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某教师调查了![]() 名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
男生 | 女生 | 总计 | |
购买数学课外辅导书超过 |
|
|
|
购买数学课外辅导书不超过 |
|
|
|
总计 |
|
|
|
(Ⅰ)根据表格中的数据,是否有![]() 的把握认为购买数学课外辅导书的数量与性别相关;
的把握认为购买数学课外辅导书的数量与性别相关;
(Ⅱ)从购买数学课外辅导书不超过![]() 本的学生中,按照性别分层抽样抽取
本的学生中,按照性别分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人询问购买原因,求恰有
人询问购买原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|