题目内容
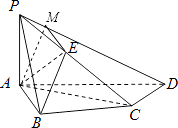
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(Ⅰ)证明:CD⊥AE;
(Ⅱ)证明:PD⊥平面ABE;
(Ⅲ)求二面角A﹣PD﹣C的正切值.
【答案】(Ⅰ)证明:在四棱锥P﹣ABCD中,PA⊥底面ABCD,CD平面ABCD,∴CD⊥PA.
又CD⊥AC,PA∩AC=A,∴CD⊥面PAC,
∵AE面PAC,故CD⊥AE.
(Ⅱ)证明:由PA=AB=BC,∠ABC=60°,可得PA=AC,
∵E是PC的中点,∴AE⊥PC,
由(1)知CD⊥AE,从而AE⊥面PCD,故AE⊥PD.
由(Ⅰ)知,AE⊥CD,且PC∩CD=C,所以AE⊥平面PCD.
而PD平面PCD,∴AE⊥PD.
∵PA⊥底面ABCD,PD在底面ABCD内的射影是AD,AB⊥AD,∴AB⊥PD.
又∵AB∩AE=A,∴PD⊥面ABE
(Ⅲ)解:过点A作AM⊥PD,垂足为M,连接EM,则(Ⅱ)知,AE⊥平面PCD,AM在平面PCD内的射影是EM,则EM⊥PD,因此∠AME是二面角A﹣PD﹣C的一个平面角.
由已知,得∠CAD=30°.设AC=a,则PA=a,AD= ![]() ,PD=
,PD= ![]() ,AE=
,AE= ![]() .
.
在直角△ADP中,∵AM⊥PD,∴AM×PD=PA×AD,∴AM= ![]() .
.
在直角△AEM中,AE= ![]() ,AM=
,AM= ![]() ,∴EM=
,∴EM= ![]() a
a
∴tan∠AME= ![]() =
= ![]() .
.
所以二面角A﹣PD﹣C的正切值为 ![]() .
.
【解析】(Ⅰ)由PA⊥底面ABCD,可得 CD⊥PA,又CD⊥AC,故CD⊥面PAC,从而证得CD⊥AE;(Ⅱ)由等腰三角形的底边中线的性质可得AE⊥PC,由(Ⅰ)知CD⊥AE,从而AE⊥面PCD,AE⊥PD,再由 AB⊥PD 可得 PD⊥面ABE;(Ⅲ)过点A作AM⊥PD,由(Ⅱ)知,AE⊥面PCD,故∠AME是二面角A﹣PD﹣C的一个平面角,用面积法求得AE和AM,从而可求 二面角A﹣PD﹣C的正切值.
【考点精析】本题主要考查了空间中直线与直线之间的位置关系和直线与平面垂直的判定的相关知识点,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.