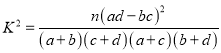题目内容
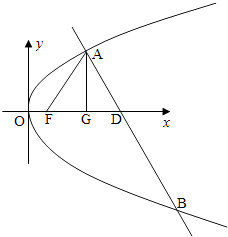
【题目】如图所示,在△ABC中,B= ![]() ,AC=2
,AC=2 ![]() ,cosC=
,cosC= ![]() .
. 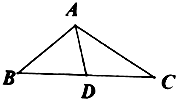
(1)求sin∠BAC的值及BC的长度;
(2)设BC的中点为D,求中线AD的长.
【答案】
(1)解:∵在△ABC中,B= ![]() ,AC=2
,AC=2 ![]() ,cosC=
,cosC= ![]() ,
,
∴sinC= ![]() =
= ![]() ,
,
∴sin∠BAC=sin(B+C)=sinBcosC+cosBsinC= ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]() ;
;
由正弦定理得: ![]() =
= ![]() ,即BC=
,即BC= ![]() =
= 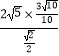 =6
=6
(2)解:在△ADC中,CD= ![]() BC=3,AC=2
BC=3,AC=2 ![]() ,cosC=
,cosC= ![]() ,
,
由余弦定理得:AD2=AC2+DC2﹣2ACDCcosC=20+9﹣2×2 ![]() ×3×
×3× ![]() =5,
=5,
则AD= ![]()
【解析】(1)由cosC的值求出sinC的值,根据诱导公式得到sin∠BAC=sin(B+C),利用两角和与差的正弦函数公式化简,将各自的值代入计算求出值,再由sin∠BAC,sinB,以及AC的长,利用正弦定理求出BC的长即可;(2)根据D为BC中点,求出CD的长,再由AC与cosC的值,利用余弦定理求出AD的长即可.
【考点精析】认真审题,首先需要了解余弦定理的定义(余弦定理:![]() ;
;![]() ;
;![]() ).
).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某教师调查了![]() 名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
男生 | 女生 | 总计 | |
购买数学课外辅导书超过 |
|
|
|
购买数学课外辅导书不超过 |
|
|
|
总计 |
|
|
|
(Ⅰ)根据表格中的数据,是否有![]() 的把握认为购买数学课外辅导书的数量与性别相关;
的把握认为购买数学课外辅导书的数量与性别相关;
(Ⅱ)从购买数学课外辅导书不超过![]() 本的学生中,按照性别分层抽样抽取
本的学生中,按照性别分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人询问购买原因,求恰有
人询问购买原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|