Question

【题目】已知正项数列的前项和为，数列满足．

（1）求数列的通项公式；

（2）数列满足，它的前项和为，

（ⅰ）求；

（ⅱ）若存在正整数，使不等式成立，求实数的取值范围．

Answer 1

【答案】（1），；（2）（ⅰ）；（ii）或．

【解析】

（1）根据已知，当时，求出，当是，利用，得到数列的递推关系，进而证明数列是等差数列，即可求出结论；

（2）（ⅰ）由数列通项公式的特征，用错位相减法求出；

（ⅱ）对分为奇数、偶数讨论，分离参数转化为存在正整数，使得或，求出最值，即可得出结论.

（1），

当时，，∴或（舍去）

当时，由，得，

两式相减得：，∴，

即，∴．

又∵数列为正项数列，故，也即，

∴数列是以1为首项，1为公差的等差数列，

∴，．

（2）（ⅰ），则

①，

②，

可得：，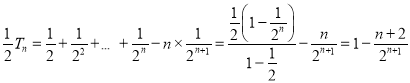

故．

（ⅱ）即不等式成立，

若为偶数，则，所以，

设，则在单调递减，

故当时，，所以；

若为奇数，则，所以

设，则在单调递增，

故当时，，所以，

综上所述，的取值范围或．