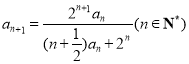题目内容
【题目】对于![]() ,若数列
,若数列![]() 满足
满足![]() ,则称这个数列为“K数列”.
,则称这个数列为“K数列”.
(Ⅰ)已知数列:1,m+1,m2是“K数列”,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在首项为-1的等差数列![]() 为“K数列”,且其前n项和
为“K数列”,且其前n项和![]() 满足
满足
![]() ?若存在,求出
?若存在,求出![]() 的通项公式;若不存在,请说明理由;
的通项公式;若不存在,请说明理由;
(Ⅲ)已知各项均为正整数的等比数列![]() 是“K数列”,数列
是“K数列”,数列![]() 不是“K数列”,若
不是“K数列”,若![]() ,试判断数列
,试判断数列![]() 是否为“K数列”,并说明理由.
是否为“K数列”,并说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析;(Ⅲ)见解析.
;(Ⅱ)见解析;(Ⅲ)见解析.
【解析】试题分析:(Ⅰ)由题意得![]() 和
和![]() ,即可求解实数
,即可求解实数![]() 的取值范围;
的取值范围;
(Ⅱ)设公差为![]() ,则
,则![]() ,得
,得![]() 对
对![]() 均成立,即
均成立,即![]() ,即可得到结论;
,即可得到结论;
(Ⅲ)设数列![]() 的公比为
的公比为![]() ,因为
,因为![]() 的每一项均为正整数,且
的每一项均为正整数,且![]() ,得到
,得到![]() ,且
,且![]() ,得到“
,得到“![]() ”和“
”和“![]() ”为最小项,又由又因为
”为最小项,又由又因为![]() 不是“K数列”, 且“
不是“K数列”, 且“![]() ”为最小项,得出
”为最小项,得出![]() ,所以
,所以![]() 或
或![]() ,分类讨论即可得到结论.
,分类讨论即可得到结论.
试题解析:(Ⅰ)由题意得![]() ,
,
![]() ,②
,②
解①得 ![]() ;
;
解②得 ![]() 或
或
所以![]() ,故实数
,故实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)假设存在等差数列![]() 符合要求,设公差为
符合要求,设公差为![]() ,则
,则![]() ,
,
由 ![]() ,得
,得 ![]() ,
,
由题意,得![]() 对
对![]() 均成立,
均成立,
即![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
因为![]() ,
,
所以![]() ,与
,与![]() 矛盾,
矛盾,
故这样的等差数列![]() 不存在.
不存在.
(Ⅲ)设数列![]() 的公比为
的公比为![]() ,则
,则![]() ,
,
因为![]() 的每一项均为正整数,且
的每一项均为正整数,且![]() ,
,
所以![]() ,且
,且![]() .
.
因为![]() ,
,
所以在![]() 中,“
中,“![]() ”为最小项.
”为最小项.
同理,在![]() 中,“
中,“![]() ”为最小项.
”为最小项.
由![]() 为“K数列”,只需
为“K数列”,只需![]() , 即
, 即 ![]() ,
,
又因为![]() 不是“K数列”, 且“
不是“K数列”, 且“![]() ”为最小项,所以
”为最小项,所以![]() , 即
, 即 ![]() ,
,
由数列![]() 的每一项均为正整数,可得
的每一项均为正整数,可得 ![]() ,
,
所以![]() 或
或![]() .
.
当![]() 时,
时,![]() , 则
, 则![]() ,
,
令![]() ,则
,则![]() ,
,
又![]()
![]() ,
,
所以![]() 为递增数列,即
为递增数列,即 ![]() ,
,
所以![]() .
.
因为![]() ,
,
所以对任意的![]() ,都有
,都有![]() ,
,
即数列![]() 为“K数列”.
为“K数列”.
当![]() 时,
时,![]() ,则
,则![]() .因为
.因为![]() ,
,
所以数列![]() 不是“K数列”.
不是“K数列”.
综上:当![]() 时,数列
时,数列![]() 为“K数列”,
为“K数列”,
当![]() 时,数列
时,数列![]() 不是“K数列” .
不是“K数列” .

【题目】某公司购买了A,B,C三种不同品牌的电动智能送风口罩.为了解三种品牌口罩的电池性能,现采用分层抽样的方法,从三种品牌的口罩中抽出25台,测试它们一次完全充电后的连续待机时长,统计结果如下(单位:小时):
A | 4 | 4 | 4.5 | 5 | 5.5 | 6 | 6 | |||
B | 4.5 | 5 | 6 | 6.5 | 6.5 | 7 | 7 | 7.5 | ||
C | 5 | 5 | 5.5 | 6 | 6 | 7 | 7 | 7.5 | 8 | 8 |
(Ⅰ)已知该公司购买的C品牌电动智能送风口罩比B品牌多200台,求该公司购买的B品牌电动智能送风口罩的数量;
(Ⅱ)从A品牌和B品牌抽出的电动智能送风口罩中,各随机选取一台,求A品牌待机时长高于B品牌的概率;
(Ⅲ)再从A,B,C三种不同品牌的电动智能送风口罩中各随机抽取一台,它们的待机时长分别是a,b,c(单位:小时).这3个新数据与表格中的数据构成的新样本的平均数记为![]() ,表格中数据的平均数记为
,表格中数据的平均数记为![]() .若
.若![]() ,写出a+b+c的最小值(结论不要求证明).
,写出a+b+c的最小值(结论不要求证明).
【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以![]() 为组距分成
为组距分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
B餐厅分数频数分布表 | |
分数区间 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|

(Ⅰ)在抽样的100人中,求对A餐厅评分低于30的人数;
(Ⅱ)从对B餐厅评分在![]() 范围内的人中随机选出2人,求2人中恰有1人评分在
范围内的人中随机选出2人,求2人中恰有1人评分在![]() 范围内的概率;
范围内的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.