Question

【题目】若函数y=f（x）满足：对y=f（x）图象上任意点P（x1 ， f（x1）），总存在点P′（x2 ， f（x2））也在y=f（x）图象上，使得x1x2+f（x1）f（x2）=0成立，称函数y=f（x）是“特殊对点函数”，给出下列五个函数：
①y=x﹣1；
②y=log2x；
③y=sinx+1；
④y=ex﹣2；
⑤y= ．
其中是“特殊对点函数”的序号是（写出所有正确的序号）

Answer 1

【答案】③④⑤
【解析】解：∵P（x1 ， f（x1）），点P′（x2 ， f（x2）），
∴若x1x2+f（x1）f（x2）=0，则等价为 =0，即 ．
①当P（1，1）时，满足 的P′（﹣1，1）不在f（x）的图象上，故①不是“特殊对点函数”，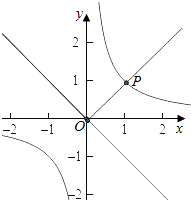

②当P（1，0）时，满足 的P′不在f（x）的图象上，故②不是“特殊对点函数”，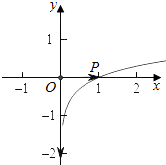

③作出函数y=sinx+1的图象，由图象知，满足 的点P′（x2 ， f（x2））都在y=f（x）图象上，则③是“特殊对点函数”，

④作出函数y=ex﹣2的图象，由图象知，满足 的点P′（x2 ， f（x2））都在y=f（x）图象上，则④是“特殊对点函数”，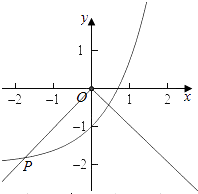

⑤作出函数y= 的图象，由图象知，满足 的点P′（x2 ， f（x2））都在y=f（x）图象上，则⑤是“特殊对点函数”．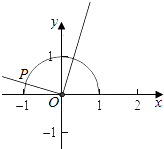

所以答案是：③④⑤
【考点精析】认真审题，首先需要了解命题的真假判断与应用(两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系)．