题目内容
7．已知p：0≤2x-1≤7，q：x2-（2a+3）x+a2+3a≤0（a为常数），（Ⅰ）若p是q的充要条件，求a的值；
（Ⅱ）若￢q是p的必要不充分条件，求a的范围．
分析 （Ⅰ）求出两个不等式的等价条件，根据若p是q的充要条件，建立方程关系即可求a的值；
（Ⅱ）求出￢q，根据￢q是p的必要不充分条件，建立不等式关系即可．
解答 解：（I）解不等式0≤2x-1≤7，
即1≤2x≤8，
得p：0≤x≤3，
解不等式x2-（2a+3）x+a2+3a≤0（a为常数），
得q：a≤x≤a+3，
若p是q的充要条件，则a=0．
（II）∵p：0≤x≤3，￢q：x＞a+3或x＜a，
∴若￢q是p的必要不充分条件，
则a＞3或a+3＜0
解得a＞3或a＜-3，
即a的范围a＞3或a＜-3．
点评 本题主要考查充分条件和必要条件的应用和判断，比较基础．
练习册系列答案
相关题目
17．已知椭圆C1与抛物线C2的焦点均在x轴上，C1的中心和C2的顶点为原点O，从椭圆C1上取两个点，从椭圆C2上取一个点，将其坐标记录于表中：
（1）试判断两个点在C1上，并求出C1，C2的标准方程；
（2）已知直线l：x=my+1与椭圆C2相交于不同两点M，N，且满足$\overrightarrow{OM}⊥\overrightarrow{ON}$，求参数m的值．
| x | $\sqrt{2}$ | 2 | 4 |
| y | $\frac{\sqrt{2}}{2}$ | 0 | 4 |
（2）已知直线l：x=my+1与椭圆C2相交于不同两点M，N，且满足$\overrightarrow{OM}⊥\overrightarrow{ON}$，求参数m的值．
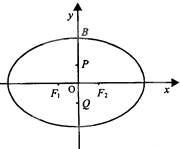如图：设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左，右两个焦点分别为F1，F2，短轴的上端点为B，短轴上的两个三等分点为P，Q，且F1PF2Q为正方形，若过点B作此正方形的外接圆的切线在x轴上的一个截距为-$\frac{3\sqrt{2}}{4}$，则此椭圆方程的方程为$\frac{x^2}{10}+\frac{y^2}{9}=1$．