题目内容
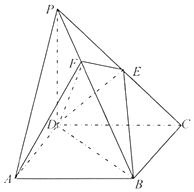
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形, ![]() ,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,E是AB中点.
,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,E是AB中点.
(Ⅰ)求证:直线AM∥平面PNC;
(Ⅱ)求证:直线CD⊥平面PDE;
(III)在AB上是否存在一点G,使得二面角G﹣PD﹣A的大小为 ![]() ,若存在,确定G的位置,若不存在,说明理由.
,若存在,确定G的位置,若不存在,说明理由.
【答案】证明:(Ⅰ)在PC上取一点F,使PF=2FC,连接MF,NF,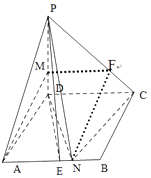
∵PM=2MD,AN=2NB,
∴MF∥DC,MF= ![]() ,AN∥DC,AN=
,AN∥DC,AN= ![]() .
.
∴MF∥AN,MF=AN,
∴MFNA为平行四边形,
即AM∥NA.
又AM平面PNC,
∴直线AM∥平面PNC;
(Ⅱ)∵E是AB中点,底面ABCD是菱形,∠DAB=60°,∴∠AED=90°.
∵AB∥CD,∴∠EDC=90°,即CD⊥DE.
又PD⊥平面ABCD,∴CD⊥PD.
又DE∩PD=D,∴直线CD⊥平面PDE;
(III)由(Ⅱ)可知DP,DE,DC,相互垂直,以D为原点,如图建立空间直角坐标系.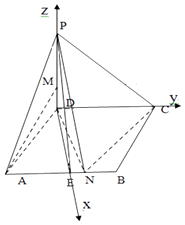
则 ![]() .
.
设面PDA的法向量 ![]() ,
,
由 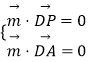 ,得
,得 ![]() .
.
设面PDG的法向量 ![]() ,
,
由  ,得
,得 ![]() .
.
∴cos60°= 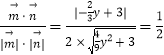 .
.
解得 ![]() ,则
,则 ![]() .
.
∴G与B重合.点B的位置为所求.
【解析】(Ⅰ)在PC上取一点F,使PF=2FC,连接MF,NF,结合已知可得MF∥DC,MF= ![]() ,AN∥DC,AN=
,AN∥DC,AN= ![]() .从而可得MFNA为平行四边形,即AM∥NA.再由线面平行的判定可得直线AM∥平面PNC;(Ⅱ)由E是AB中点,底面ABCD是菱形,∠DAB=60°,得∠AED=90°.进一步得到CD⊥DE.再由PD⊥平面ABCD得CD⊥PD.由线面垂直的判定可得直线CD⊥平面PDE;(III)由(Ⅱ)可知DP,DE,DC,相互垂直,以D为原点,建立空间直角坐标系.然后利用平面法向量所成角的余弦值求得G点位置.
.从而可得MFNA为平行四边形,即AM∥NA.再由线面平行的判定可得直线AM∥平面PNC;(Ⅱ)由E是AB中点,底面ABCD是菱形,∠DAB=60°,得∠AED=90°.进一步得到CD⊥DE.再由PD⊥平面ABCD得CD⊥PD.由线面垂直的判定可得直线CD⊥平面PDE;(III)由(Ⅱ)可知DP,DE,DC,相互垂直,以D为原点,建立空间直角坐标系.然后利用平面法向量所成角的余弦值求得G点位置.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面垂直的判定的理解,了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某成衣批发店为了对一款成衣进行合理定价,将该款成衣按事先拟定的价格进行试销,得到了如下数据:
批发单价x(元) | 80 | 82 | 84 | 86 | 88 | 90 |
销售量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() ,其中
,其中 ![]()
(2)预测批发单价定为85元时,销售量大概是多少件?
(3)假设在今后的销售中,销售量与批发单价仍然服从(1)中的关系,且该款成衣的成本价为40元/件,为使该成衣批发店在该款成衣上获得更大利润,该款成衣单价大约定为多少元?