题目内容
(本小题满分12分)



如图,A为椭圆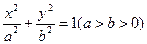 上
上
 的一个动点,弦AB、AC分别过焦点
的一个动点,弦AB、AC分别过焦点
F1、F2。当AC垂直于x轴时,恰好
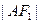 ∶
∶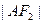 =3∶1.(1)求该椭圆的离心率;
=3∶1.(1)求该椭圆的离心率;
(2)设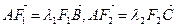 ,试判断
,试判断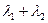 是否为定值?若是,则求出该定值;若不是,请说明理由。
是否为定值?若是,则求出该定值;若不是,请说明理由。



|
|
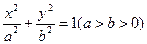 上
上
|
|
 的一个动点,弦AB、AC分别过焦点
的一个动点,弦AB、AC分别过焦点
|
|
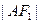 ∶
∶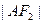 =3∶1.(1)求该椭圆的离心率;
=3∶1.(1)求该椭圆的离心率;(2)设
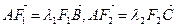 ,试判断
,试判断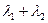 是否为定值?若是,则求出该定值;若不是,请说明理由。
是否为定值?若是,则求出该定值;若不是,请说明理由。(1) 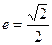
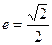
(1)当AC垂直于x轴时,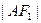 ∶
∶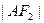 =3∶1
=3∶1

由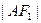 +
+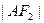 =2a,得
=2a,得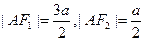 ……2分在Rt△AF1F2中,
……2分在Rt△AF1F2中,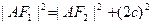

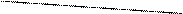


 【或由
【或由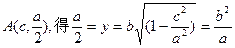 】
】
解得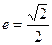 ……4分(2)由
……4分(2)由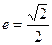 ,则
,则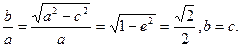 ,
,
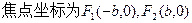 ,则椭圆方程为
,则椭圆方程为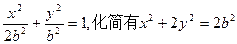 .
.
设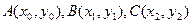 ,①若直线AC的斜率存在,则直线AC方程为
,①若直线AC的斜率存在,则直线AC方程为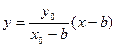 ,代入椭圆方程有
,代入椭圆方程有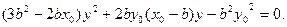
由韦达定理得: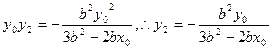 ……7分
……7分
所以
故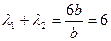 ……9分
……9分
②若直线AC⊥x轴,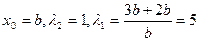 ∴
∴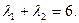 ……11分
……11分
综上所述: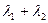 是定值6……12分
是定值6……12分
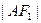 ∶
∶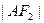 =3∶1
=3∶1
|
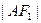 +
+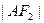 =2a,得
=2a,得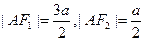 ……2分在Rt△AF1F2中,
……2分在Rt△AF1F2中,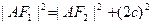
|
|
|
|
|
|



 【或由
【或由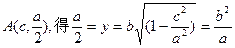 】
】
|
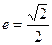 ……4分(2)由
……4分(2)由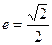 ,则
,则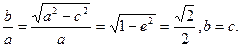 ,
,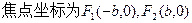 ,则椭圆方程为
,则椭圆方程为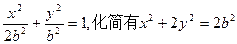 .
.设
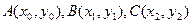 ,①若直线AC的斜率存在,则直线AC方程为
,①若直线AC的斜率存在,则直线AC方程为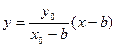 ,代入椭圆方程有
,代入椭圆方程有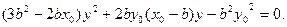
由韦达定理得:
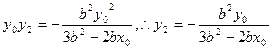 ……7分
……7分所以

故
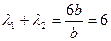 ……9分
……9分②若直线AC⊥x轴,
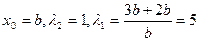 ∴
∴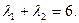 ……11分
……11分综上所述:
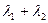 是定值6……12分
是定值6……12分
练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
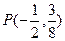 和到直线
和到直线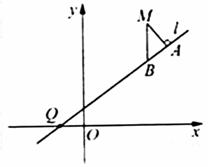
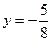 距离相等的点的轨迹,l是过点Q(-1,0)的直线,
距离相等的点的轨迹,l是过点Q(-1,0)的直线,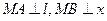
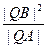 为常数。
为常数。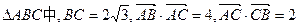 ,双曲线M是以B、C为焦点且过A点.(Ⅰ)建立适当的坐标系,求双曲线M的方程;(Ⅱ)设过点E(1,0)的直线l分别与双曲线M的左、右支交于F、G两点,直线l的斜率为k,求k的取值范围.;
,双曲线M是以B、C为焦点且过A点.(Ⅰ)建立适当的坐标系,求双曲线M的方程;(Ⅱ)设过点E(1,0)的直线l分别与双曲线M的左、右支交于F、G两点,直线l的斜率为k,求k的取值范围.;
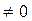 使|OF|=|OG|
使|OF|=|OG|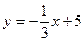 与曲线
与曲线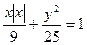 的交点个数是 ( )
的交点个数是 ( ) 0个 B
0个 B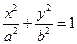
 的中心.椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行。又抛物线与椭圆交于点
的中心.椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行。又抛物线与椭圆交于点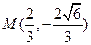 ,求抛物线与椭圆的方程.
,求抛物线与椭圆的方程. 已知椭圆
已知椭圆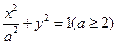 ,直线
,直线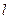 与椭圆交于
与椭圆交于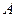 、
、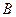 两点,
两点,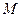 是线段
是线段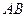 的中点,连接
的中点,连接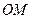 并延长交椭圆于点
并延长交椭圆于点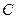 .
.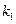 、
、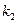 ,且
,且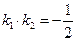 ,求椭圆的离心率.若直线
,求椭圆的离心率.若直线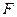 ,且四边形
,且四边形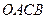 是平行四边形,求直线
是平行四边形,求直线
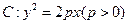 上任意一点到焦点F的距离比到
上任意一点到焦点F的距离比到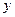 轴的距离大1,(1)求抛物线C的方程;(2)若过焦点F的直线交抛物线于M,N两点,M在第一象限,且
轴的距离大1,(1)求抛物线C的方程;(2)若过焦点F的直线交抛物线于M,N两点,M在第一象限,且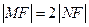 ,求直线MN的方程;(3)过点
,求直线MN的方程;(3)过点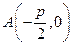 的直线交抛物线
的直线交抛物线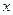 轴的对称点为R,求证:直线RQ必过定点.
轴的对称点为R,求证:直线RQ必过定点.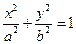
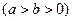 的左、右焦点分别为
的左、右焦点分别为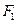 、
、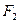 ,抛物线
,抛物线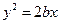 的焦点为
的焦点为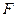 .若
.若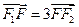 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )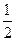 B.
B.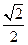 C.
C.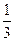 D.
D.