题目内容
(本小题满分16分)
已知函数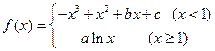 的图象过点
的图象过点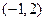 ,且在点
,且在点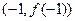 处的切线与直线
处的切线与直线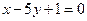 垂直.
垂直.
(1) 求实数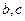 的值; (6分)
的值; (6分)
(2) 求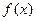 在
在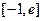 (
(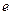 为自然对数的底数)上的最大值; (5分)
为自然对数的底数)上的最大值; (5分)
(3) 对任意给定的正实数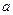 ,曲线
,曲线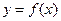 上是否存在两点
上是否存在两点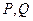 ,使得
,使得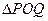 是以
是以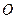 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在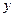 轴上? (5分)
轴上? (5分)
已知函数
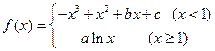 的图象过点
的图象过点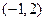 ,且在点
,且在点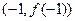 处的切线与直线
处的切线与直线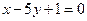 垂直.
垂直.(1) 求实数
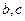 的值; (6分)
的值; (6分)(2) 求
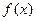 在
在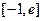 (
(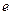 为自然对数的底数)上的最大值; (5分)
为自然对数的底数)上的最大值; (5分)(3) 对任意给定的正实数
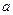 ,曲线
,曲线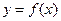 上是否存在两点
上是否存在两点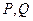 ,使得
,使得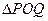 是以
是以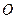 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在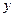 轴上? (5分)
轴上? (5分)(1)当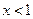 时,
时,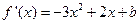 , ………2分
, ………2分
由题意得: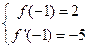 ,即
,即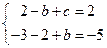 , ………4分
, ………4分
解得: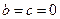 。 ………6分
。 ………6分
(2)由(1)知: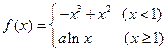
①当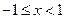 时,
时,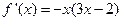 ,
,
解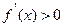 得
得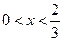 ;解
;解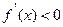 得
得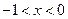 或
或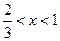
∴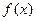 在
在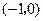 和
和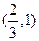 上单减,在
上单减,在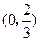 上单增,
上单增,
由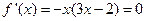 得:
得: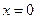 或
或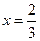 , ………7分
, ………7分
∵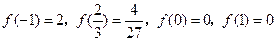 ,
,
∴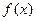 在
在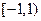 上的最大值为
上的最大值为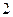 。
。
②当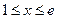 时,
时,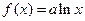 ,
,
当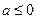 时,
时,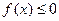 ;当
;当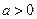 时,
时,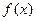 在
在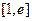 单调递增;
单调递增;
∴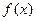 在
在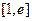 上的最大值为
上的最大值为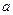 。 --……9分
。 --……9分
∴当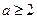 时,
时,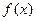 在
在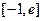 上的最大值为
上的最大值为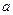 ;
;
当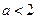 时,
时,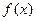 在
在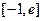 上的最大值为
上的最大值为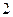 。 …………11分
。 …………11分
(3)假设曲线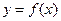 上存在两点
上存在两点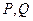 满足题意,则
满足题意,则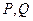 只能在
只能在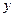 轴两侧,不妨设
轴两侧,不妨设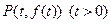 ,则
,则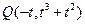 ,且
,且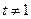 。
。
∵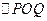 是以
是以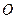 为直角顶点的直角三角形
为直角顶点的直角三角形
∴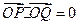 ,即
,即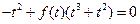 (*) ……13分
(*) ……13分
是否存在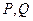 等价于方程(*)是否有解。
等价于方程(*)是否有解。
①若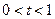 ,则
,则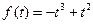 ,代入方程(*)得:
,代入方程(*)得: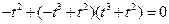 ,
,
即: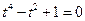 ,而此方程无实数解,从而
,而此方程无实数解,从而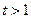 ,
,
∴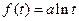 ,代入方程(*)得:
,代入方程(*)得: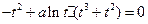 ,
,
即: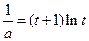 ,
,
设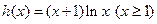 ,则
,则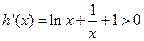 在
在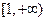 恒成立,
恒成立,
∴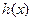 在
在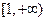 上单调递增,从而
上单调递增,从而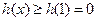 ,则
,则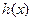 的值域为
的值域为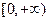 。
。
∴当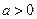 时,方程
时,方程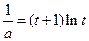 有解,即方程(*)有解。
有解,即方程(*)有解。
∴对任意给定的正实数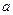 ,曲线
,曲线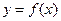 上总存在两点
上总存在两点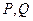 ,
,
使得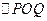 是以
是以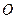 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在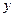 轴
轴
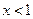 时,
时,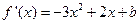 , ………2分
, ………2分由题意得:
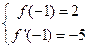 ,即
,即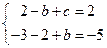 , ………4分
, ………4分解得:
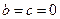 。 ………6分
。 ………6分(2)由(1)知:
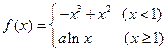
①当
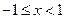 时,
时,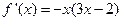 ,
,解
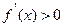 得
得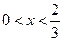 ;解
;解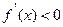 得
得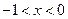 或
或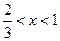
∴
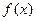 在
在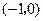 和
和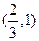 上单减,在
上单减,在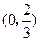 上单增,
上单增,由
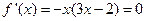 得:
得: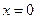 或
或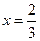 , ………7分
, ………7分∵
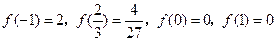 ,
,∴
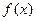 在
在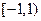 上的最大值为
上的最大值为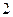 。
。 ②当
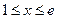 时,
时,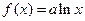 ,
,当
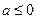 时,
时,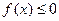 ;当
;当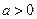 时,
时,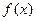 在
在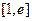 单调递增;
单调递增;∴
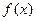 在
在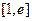 上的最大值为
上的最大值为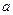 。 --……9分
。 --……9分∴当
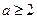 时,
时,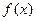 在
在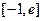 上的最大值为
上的最大值为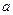 ;
;当
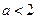 时,
时,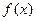 在
在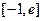 上的最大值为
上的最大值为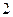 。 …………11分
。 …………11分(3)假设曲线
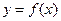 上存在两点
上存在两点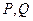 满足题意,则
满足题意,则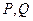 只能在
只能在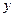 轴两侧,不妨设
轴两侧,不妨设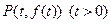 ,则
,则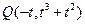 ,且
,且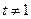 。
。∵
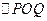 是以
是以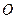 为直角顶点的直角三角形
为直角顶点的直角三角形∴
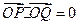 ,即
,即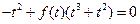 (*) ……13分
(*) ……13分是否存在
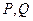 等价于方程(*)是否有解。
等价于方程(*)是否有解。①若
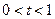 ,则
,则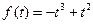 ,代入方程(*)得:
,代入方程(*)得: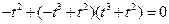 ,
,即:
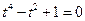 ,而此方程无实数解,从而
,而此方程无实数解,从而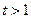 ,
, ∴
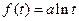 ,代入方程(*)得:
,代入方程(*)得: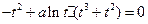 ,
,即:
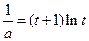 ,
, 设
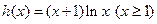 ,则
,则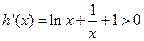 在
在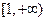 恒成立,
恒成立,∴
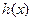 在
在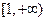 上单调递增,从而
上单调递增,从而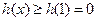 ,则
,则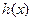 的值域为
的值域为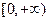 。
。∴当
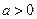 时,方程
时,方程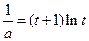 有解,即方程(*)有解。
有解,即方程(*)有解。∴对任意给定的正实数
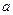 ,曲线
,曲线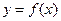 上总存在两点
上总存在两点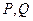 ,
,使得
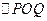 是以
是以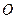 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在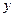 轴
轴略

练习册系列答案
相关题目
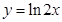 在
在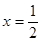 处的切线方程是 ( )
处的切线方程是 ( )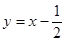
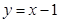
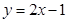
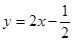
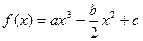 ,其图像过点(0,1).
,其图像过点(0,1).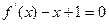 的两个根分别为是
的两个根分别为是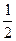 ,1时,求f(x)的解析式;
,1时,求f(x)的解析式;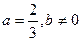 时,求函数f(x)的极大值与极小值.
时,求函数f(x)的极大值与极小值.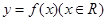 上任一点
上任一点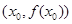 处的切线斜率
处的切线斜率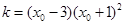 ,则该函数的单调递减区间为
,则该函数的单调递减区间为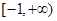
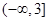
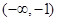
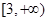
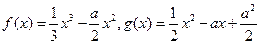 。
。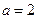 时,求曲线
时,求曲线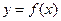 在点
在点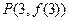 处的切线方程;
处的切线方程;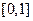 上的最小值为
上的最小值为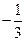 时,求实数
时,求实数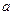 的值;
的值;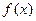 与
与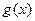 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数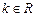 ,函数
,函数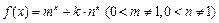 .
.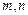 满足
满足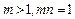 ,函数
,函数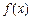 是否具有奇偶性?如果有,求出相应的
是否具有奇偶性?如果有,求出相应的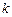
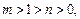 判断函数
判断函数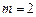 ,
,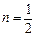 ,且
,且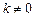 ,求函数
,求函数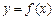 的对称轴或对称中心.
的对称轴或对称中心.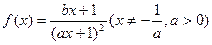 ,且
,且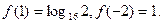
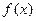 的表达式;
的表达式;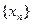 的项满足
的项满足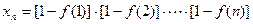 ,试求
,试求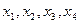 ;
;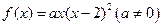 有极大值
有极大值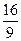 ,则
,则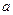 等于
等于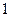

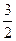
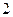 (
(

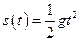 (
(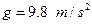 ),则
),则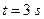 时的瞬时速度为( )
时的瞬时速度为( )