题目内容
设函数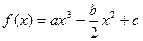 ,其图像过点(0,1).
,其图像过点(0,1).
(1)当方程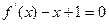 的两个根分别为是
的两个根分别为是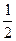 ,1时,求f(x)的解析式;
,1时,求f(x)的解析式;
(2)当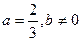 时,求函数f(x)的极大值与极小值.
时,求函数f(x)的极大值与极小值.
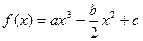 ,其图像过点(0,1).
,其图像过点(0,1).(1)当方程
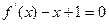 的两个根分别为是
的两个根分别为是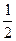 ,1时,求f(x)的解析式;
,1时,求f(x)的解析式;(2)当
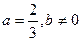 时,求函数f(x)的极大值与极小值.
时,求函数f(x)的极大值与极小值. 解:由题意可知,f(0)=1所以c="1 "
解:由题意可知,f(0)=1所以c="1 "  ………… ………………………. ……………………….1分
………… ………………………. ……………………….1分(Ⅰ)
 由
由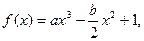 得
得
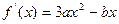

 .
.因为
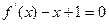 ,即
,即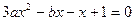 的两个根分别为
的两个根分别为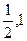

所以

 解得
解得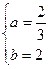
故
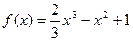

 ………… ………………………. ……………………….6分
………… ………………………. ……………………….6分(Ⅱ)

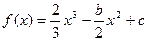
所以,

 ………… ………………………. ……………………….7分
………… ………………………. ……………………….7分①若b>0,则当
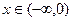 时,
时,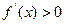 函数f(x)单调递增
函数f(x)单调递增

 当
当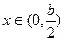 时,
时,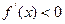 函数f(x)单调递减
函数f(x)单调递减 当
当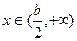 时,
时,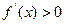 函数f(x)单调递增
函数f(x)单调递增
因此,f(x)的极大值为f(0)="c=1,"
f(x)的极小值为
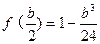 ……… ………………………. ……………………….10分
……… ………………………. ……………………….10分②若b<0,则当
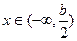 时,
时,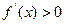 函数f(x)单调递增
函数f(x)单调递增

 当
当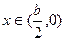 时,
时,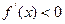 函数f(x)单调递减
函数f(x)单调递减 当
当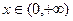 时,
时,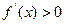 函数f(x)单调递增
函数f(x)单调递增
因此,f(x)的极大值为
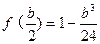
f(x)的极小值为f(0)=1.
综上所述,当b>0时, f(x)的极大值为1, 极小值为
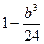 ,
,当b<0时, f(x)的极大值为
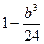 , 极小值为
, 极小值为 1. ………………. ……………………….13分
1. ………………. ……………………….13分略

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
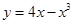 在点(-1,-3)处的切线方程是 ( )
在点(-1,-3)处的切线方程是 ( )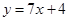 B
B 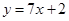 C
C 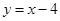 D
D 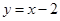
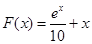 的作用,(x 的单位:m, F的单位:N),则它从
的作用,(x 的单位:m, F的单位:N),则它从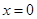 运动到
运动到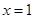 时
时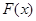 所做的功等于 J。
所做的功等于 J。 (
(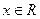 ),其中
),其中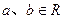 .
.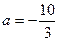 时,讨论函数
时,讨论函数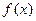 的单调性;
的单调性;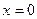 处有极值,求
处有极值,求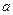 的取值范围;
的取值范围;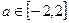 ,不等式
,不等式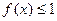 在
在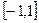 上恒成立,求
上恒成立,求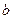 的取值范围.
的取值范围.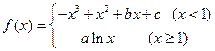 的图象过点
的图象过点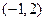 ,且在点
,且在点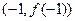 处的切线与直线
处的切线与直线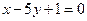 垂直.
垂直.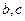 的值; (6分)
的值; (6分)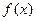 在
在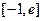 (
(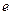 为自然对数的底数)上的最大值; (5分)
为自然对数的底数)上的最大值; (5分)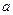 ,曲线
,曲线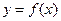 上是否存在两点
上是否存在两点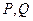 ,使得
,使得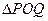 是以
是以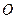 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在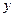 轴上? (5分)
轴上? (5分)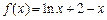 ,若
,若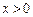 ,
,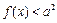 恒成立,则实数
恒成立,则实数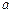 的取值范围是 .
的取值范围是 .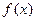 的二次项系数为a,且不等式
的二次项系数为a,且不等式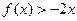 的解集为(1,3)。
的解集为(1,3)。 若方程
若方程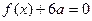 有两个相等的实数根,求
有两个相等的实数根,求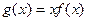 无极值,求实数
无极值,求实数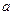 的取值范围。
的取值范围。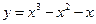 的单调增区间为______________________________。
的单调增区间为______________________________。