题目内容
已知函数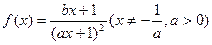 ,且
,且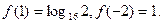
(1)求函数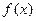 的表达式;
的表达式;
(2)若数列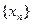 的项满足
的项满足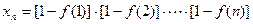 ,试求
,试求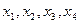 ;
;
(3)猜想数列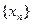 的通项,并用数学归纳法证明.
的通项,并用数学归纳法证明.
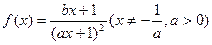 ,且
,且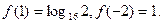
(1)求函数
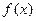 的表达式;
的表达式;(2)若数列
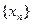 的项满足
的项满足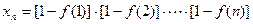 ,试求
,试求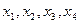 ;
;(3)猜想数列
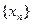 的通项,并用数学归纳法证明.
的通项,并用数学归纳法证明.解:(1)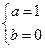
(2)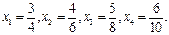
(3)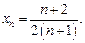 用数学归纳法证明.
用数学归纳法证明.
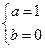
(2)
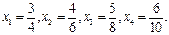
(3)
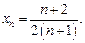 用数学归纳法证明.
用数学归纳法证明.略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
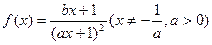 ,且
,且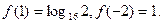
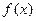 的表达式;
的表达式;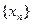 的项满足
的项满足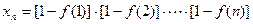 ,试求
,试求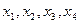 ;
;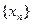 的通项,并用数学归纳法证明.
的通项,并用数学归纳法证明.
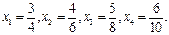
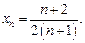 用数学归纳法证明.
用数学归纳法证明.
 名校课堂系列答案
名校课堂系列答案