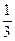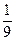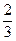题目内容
曲线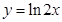 在
在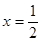 处的切线方程是 ( )
处的切线方程是 ( )
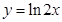 在
在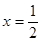 处的切线方程是 ( )
处的切线方程是 ( )A.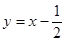 | B.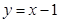 | C.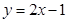 | D.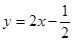 |
C
分析:利用切线方程,结合导数的几何意义,求出切线的斜率,即可求得切线方程.
解答:解:由y=ln2x可得y′=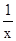
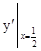 =2=k,又切点为(
=2=k,又切点为( ,0),由直线的点斜式方程得:y-0=2(x-
,0),由直线的点斜式方程得:y-0=2(x- ),整理得y=2x-1
),整理得y=2x-1
故选C.
点评:本题考查导数的几何意义,考查曲线的切线,考查学生的计算能力,属于基础题.
解答:解:由y=ln2x可得y′=
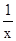
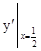 =2=k,又切点为(
=2=k,又切点为( ,0),由直线的点斜式方程得:y-0=2(x-
,0),由直线的点斜式方程得:y-0=2(x- ),整理得y=2x-1
),整理得y=2x-1故选C.
点评:本题考查导数的几何意义,考查曲线的切线,考查学生的计算能力,属于基础题.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
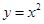 在点P处的切线的倾斜角为
在点P处的切线的倾斜角为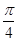 ,则P点坐标为 ( )
,则P点坐标为 ( )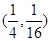
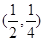
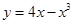 在点(-1,-3)处的切线方程是 ( )
在点(-1,-3)处的切线方程是 ( )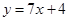 B
B 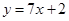 C
C 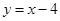 D
D 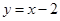
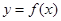 的导函数
的导函数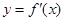 的图象,下列说法错误的是…………( )
的图象,下列说法错误的是…………( )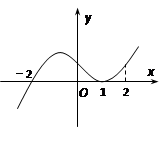
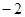 是函数
是函数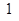 是函数
是函数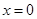 处切线的斜率大于零;
处切线的斜率大于零;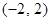 上单调递增.
上单调递增.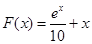 的作用,(x 的单位:m, F的单位:N),则它从
的作用,(x 的单位:m, F的单位:N),则它从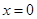 运动到
运动到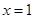 时
时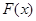 所做的功等于 J。
所做的功等于 J。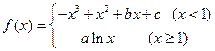 的图象过点
的图象过点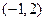 ,且在点
,且在点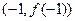 处的切线与直线
处的切线与直线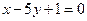 垂直.
垂直.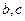 的值; (6分)
的值; (6分)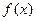 在
在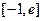 (
(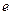 为自然对数的底数)上的最大值; (5分)
为自然对数的底数)上的最大值; (5分)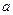 ,曲线
,曲线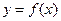 上是否存在两点
上是否存在两点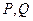 ,使得
,使得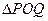 是以
是以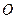 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在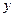 轴上? (5分)
轴上? (5分) 是曲线
是曲线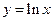 的切线, 则
的切线, 则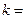 __________;
__________;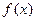 的二次项系数为a,且不等式
的二次项系数为a,且不等式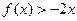 的解集为(1,3)。
的解集为(1,3)。 若方程
若方程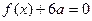 有两个相等的实数根,求
有两个相等的实数根,求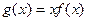 无极值,求实数
无极值,求实数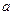 的取值范围。
的取值范围。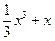 在点(1,
在点(1,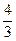 )处的切线与坐标轴围成的三角形面积为( )
)处的切线与坐标轴围成的三角形面积为( )