题目内容
(本题满分16分)
已知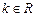 ,函数
,函数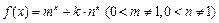 .
.
(1) 如果实数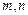 满足
满足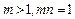 ,函数
,函数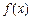 是否具有奇偶性?如果有,求出相应的
是否具有奇偶性?如果有,求出相应的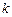
值,如果没有,说明为什么?
(2) 如果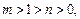 判断函数
判断函数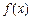 的单调性;
的单调性;
(3) 如果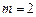 ,
,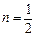 ,且
,且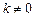 ,求函数
,求函数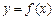 的对称轴或对称中心.
的对称轴或对称中心.
已知
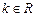 ,函数
,函数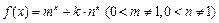 .
.(1) 如果实数
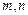 满足
满足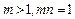 ,函数
,函数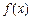 是否具有奇偶性?如果有,求出相应的
是否具有奇偶性?如果有,求出相应的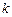
值,如果没有,说明为什么?
(2) 如果
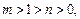 判断函数
判断函数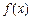 的单调性;
的单调性;(3) 如果
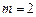 ,
,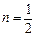 ,且
,且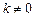 ,求函数
,求函数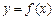 的对称轴或对称中心.
的对称轴或对称中心..(16分)

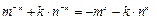 恒成立,(4分)
恒成立,(4分)
即:
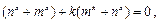 (5分)
(5分)
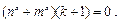 由
由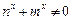 恒成立,得
恒成立,得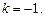 (6分)
(6分)
(2)
 ,
,
∴ 当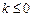 时,显然
时,显然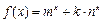 在R上为增函数;(8分)
在R上为增函数;(8分)
当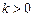 时,
时, ,
,
由 得
得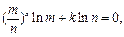 得
得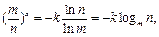
得 .(9分)
.(9分)
∴当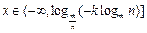 时,
时, 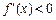 ,
,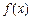 为减函数; (10分)
为减函数; (10分)
当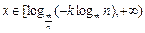 时,
时, 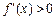 ,
,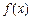 为增函数. (11分)
为增函数. (11分)
(3) 当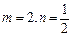 时,
时,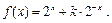
如果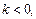
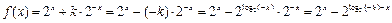 ,(13分)
,(13分)
则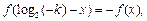
∴函数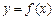 有对称中心
有对称中心 (14分)
(14分)
如果
 (15分)
(15分)
则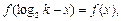
∴函数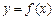 有对称轴
有对称轴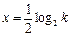 .(16分)
.(16分)

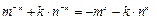 恒成立,(4分)
恒成立,(4分)即:

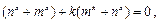 (5分)
(5分)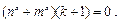 由
由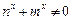 恒成立,得
恒成立,得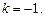 (6分)
(6分)(2)

 ,
,∴ 当
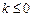 时,显然
时,显然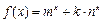 在R上为增函数;(8分)
在R上为增函数;(8分)当
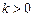 时,
时, ,
,由
 得
得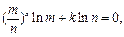 得
得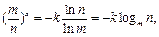
得
 .(9分)
.(9分)∴当
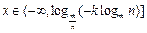 时,
时, 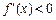 ,
,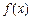 为减函数; (10分)
为减函数; (10分)当
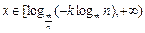 时,
时, 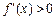 ,
,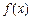 为增函数. (11分)
为增函数. (11分)(3) 当
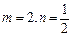 时,
时,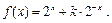
如果
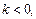
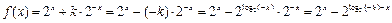 ,(13分)
,(13分)则
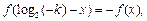
∴函数
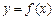 有对称中心
有对称中心 (14分)
(14分)如果

 (15分)
(15分)则
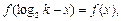
∴函数
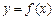 有对称轴
有对称轴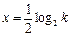 .(16分)
.(16分)略

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
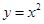 在点P处的切线的倾斜角为
在点P处的切线的倾斜角为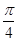 ,则P点坐标为 ( )
,则P点坐标为 ( )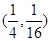
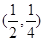
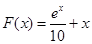 的作用,(x 的单位:m, F的单位:N),则它从
的作用,(x 的单位:m, F的单位:N),则它从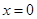 运动到
运动到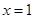 时
时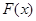 所做的功等于 J。
所做的功等于 J。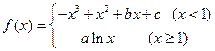 的图象过点
的图象过点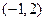 ,且在点
,且在点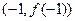 处的切线与直线
处的切线与直线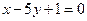 垂直.
垂直.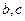 的值; (6分)
的值; (6分)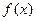 在
在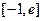 (
(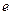 为自然对数的底数)上的最大值; (5分)
为自然对数的底数)上的最大值; (5分)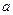 ,曲线
,曲线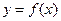 上是否存在两点
上是否存在两点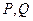 ,使得
,使得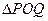 是以
是以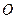 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在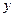 轴上? (5分)
轴上? (5分)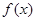 是定义在R上的奇函数,
是定义在R上的奇函数,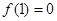 ,
,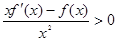
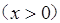 ,
,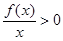 的解集是 .
的解集是 . 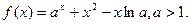
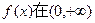 上单调递增;
上单调递增;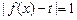 有三个不同的实根,求t的值;
有三个不同的实根,求t的值; 的取值范围。
的取值范围。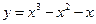 的单调增区间为______________________________。
的单调增区间为______________________________。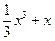 在点(1,
在点(1,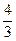 )处的切线与坐标轴围成的三角形面积为( )
)处的切线与坐标轴围成的三角形面积为( )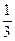


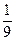
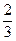

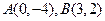 ,抛物线
,抛物线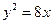 上的点到直线
上的点到直线 的最短距离___ 。
的最短距离___ 。