题目内容
【题目】某国建了一座时间机器,形似一条圆形地铁轨道,其上均匀设置了2014个站台(编号依次为l,2,…,2014)分别对应一个年份,起始站及终点站均为第1站(对应2014年).为节约成本,机器每次运行一圈,只在其中一半的站台停靠,出于技术原因,每次至多行驶三站必须停靠一次,且所停靠的任两个站台不能是圆形轨道的对径点.试求不同的停靠方式的种数.
【答案】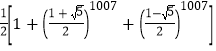
【解析】
令![]() .设不同的停靠方式共有
.设不同的停靠方式共有![]() 种.
种.
首先,对每种停靠方式,定义停靠的站为![]() 类,未停靠的站为
类,未停靠的站为![]() 类,则
类,则![]() 类站与
类站与![]() 类站一一配对,组成对径点.
类站一一配对,组成对径点.
显然,不存在相邻的三个![]() 类站(否则,设
类站(否则,设![]() 、
、![]() 、
、![]() 为相邻的
为相邻的![]() 类站,则其对径点
类站,则其对径点![]() 、
、![]() 、
、![]() 为相邻的
为相邻的![]() 类站,机器没有停靠,与题设矛盾),且第1站为
类站,机器没有停靠,与题设矛盾),且第1站为![]() 类,第
类,第![]() 站为
站为![]() 类.
类.
从而,每种停靠方式对应一种第![]() 站的分类方式(第
站的分类方式(第![]() 站的分类方式由第
站的分类方式由第![]() 站的分类方式唯一确定),使得没有相邻三站同类.
站的分类方式唯一确定),使得没有相邻三站同类.
接下来,考虑连续![]() 个站台的分类方式(其中,首尾两站为
个站台的分类方式(其中,首尾两站为![]() 类,且没有相邻三站同类).设其分类方式种数为
类,且没有相邻三站同类).设其分类方式种数为![]() .
.
显然,![]() ,
,![]() ,
,![]() ,
,![]() .
.
对![]() ,考虑最末两个
,考虑最末两个![]() 类站中间的
类站中间的![]() 类站的个数
类站的个数![]() .若
.若![]() ,则分类种数为
,则分类种数为![]() ;若
;若![]() ,则分类种数为
,则分类种数为![]() ;若
;若![]() ,则与其相邻站为
,则与其相邻站为![]() 类,分类种数为
类,分类种数为![]() .
.
故![]() .②
.②
设![]() .③
.③
则![]()
![]()
![]() ④
④
由结论①和式②得![]() .则
.则![]() ,
,![]() .
.
由式④知![]() 为第
为第![]() 个斐波那契数
个斐波那契数![]() ,即
,即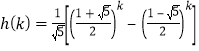 .
.
由式③得![]() ,
,
![]() ,
,
![]() .
.
其次,计算第![]() 站的分类种数
站的分类种数![]() .
.
若![]() 为
为![]() 类,则相应分类种数为
类,则相应分类种数为![]() .
.
若![]() 为
为![]() 类,则
类,则![]() 、
、![]() 为
为![]() 类,2为
类,2为![]() 类.
类.
如果3为![]() 类,则相应分类种数为
类,则相应分类种数为![]() ;
;
如果3为![]() 类,则4为
类,则4为![]() 类,相应分类种数为
类,相应分类种数为![]() .
.
故![]() .
.
最后,求![]() .
.
![]()
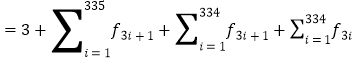
![]()
![]() .
.
由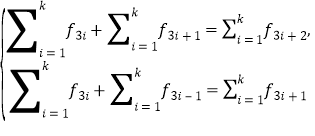
![]() .
.
故![]()
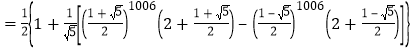
 .
.

 阅读快车系列答案
阅读快车系列答案【题目】某服装公司,为确定明年![]() 类服装的广告费用,对往年广告费
类服装的广告费用,对往年广告费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:件)和年利润
(单位:件)和年利润![]() (单位:千元)的影响.对2011-2018广告费
(单位:千元)的影响.对2011-2018广告费![]() 和年销售量
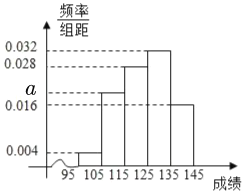
和年销售量![]() 数据进行了处理,分析出以下散点图和统计量:
数据进行了处理,分析出以下散点图和统计量:

|
|
|
|
|
|
|
45 | 580 | 2025 | 297 | 1600 | 960 | 1440 |
表中![]()
(1)由散点图可知,![]() 和
和![]() 更适合作为年销售量
更适合作为年销售量![]() 关于年广告费
关于年广告费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果和表中数据求![]() 关于
关于![]() 的回归方程.
的回归方程.
(3)已知该类服装年利率![]() 与
与![]() 的关系为
的关系为![]() .由(2)回答以下问题:年广告费用
.由(2)回答以下问题:年广告费用![]() 等于60时,年销售量及年利润的预报值为多少?年广告费用为何值时,年利率的预报值最小?
等于60时,年销售量及年利润的预报值为多少?年广告费用为何值时,年利率的预报值最小?
对于一组数据![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
【题目】某面包店推出一款新面包,每个面包的成本价为![]() 元,售价为
元,售价为![]() 元,该款面包当天只出一炉(一炉至少
元,该款面包当天只出一炉(一炉至少![]() 个,至多
个,至多![]() 个),当天如果没有售完,剩余的面包以每个
个),当天如果没有售完,剩余的面包以每个![]() 元的价格处理掉,为了确定这一炉面包的个数,以便利润最大化,该店记录了这款新面包最近
元的价格处理掉,为了确定这一炉面包的个数,以便利润最大化,该店记录了这款新面包最近![]() 天的日需求量(单位:个),整理得下表:
天的日需求量(单位:个),整理得下表:
日需求量 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该店这款新面包每日出炉数设定为![]() 个
个
(i)求日需求量为![]() 个时的当日利润;
个时的当日利润;
(ii)求这![]() 天的日均利润.
天的日均利润.
相关公式: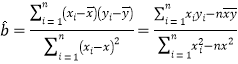 ,
,![]()