题目内容
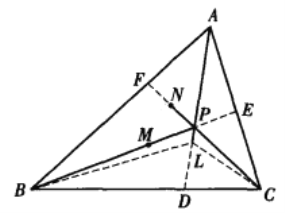
【题目】如图,设L、M、N分别为![]() 的∠BAC、∠ CBA、∠ ACB内的点,且∠BAL=∠ ACL,∠ LBA=∠ LAC,∠ CBM=∠ BAM,∠ MCB=∠ MBA,∠ ACN=∠ CBN,∠ NAC=∠ NCB.
的∠BAC、∠ CBA、∠ ACB内的点,且∠BAL=∠ ACL,∠ LBA=∠ LAC,∠ CBM=∠ BAM,∠ MCB=∠ MBA,∠ ACN=∠ CBN,∠ NAC=∠ NCB.

证明:(1) AL、BM、CN三线交于一点P;
(2)L、M、N、P四点共圆.
【答案】(1)见解析;(2)见解析
【解析】
(1)如图,设AL与BC交于点D,BM与CA交于点E,CN与AB交于点F.
由∠BAL=∠ACL,∠ABL=∠CAL,得![]() .
.
由∠BLD=∠BAL+∠LBA=∠ACL+∠LAC=∠DLC
即LD平分∠BLC,得![]() .
.
类似地,![]() ,
,![]() .
.
故![]() .
.
由塞瓦定理,知AD、BE、CF三线共点,即AL、BM、CN三线共点,记交点为P.
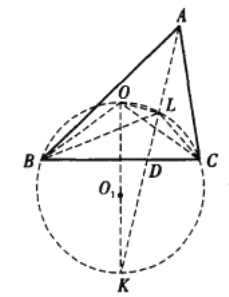
(2)如图,记![]() 的外心为O.注意到,∠BAC=∠ACL,∠LBA=∠LAC
的外心为O.注意到,∠BAC=∠ACL,∠LBA=∠LAC
则![]() .
.
于是,B、O、L、C四点共圆,即点O在![]() 的外接圆上.
的外接圆上.
因为AD平分∠BLC,所以,直线AD与BC的垂直平分线的交点为![]() 的外接圆的弧
的外接圆的弧![]() (不含点L)的中点K.
(不含点L)的中点K.
故OK为![]() 外接圆的直径,
外接圆的直径,![]() ,即∠OLP=90°.
,即∠OLP=90°.
类似地,∠OMP=90°,∠ONP=90°.
因此,点L、M、N均在以OP为直径的圆上,L、M、N、P四点共圆.

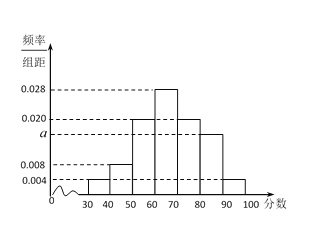
【题目】改革开放40年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各50人,进行问卷测评,所得分数的频率分布直方图如图所示.规定得分在80分以上为交通安全意识强.
安全意识强 | 安全意识不强 | 合计 | |
男性 | |||
女性 | |||
合计 |
(Ⅰ)求![]() 的值,并估计该城市驾驶员交通安全意识强的概率;
的值,并估计该城市驾驶员交通安全意识强的概率;
(Ⅱ)已知交通安全意识强的样本中男女比例为4:1,完成2×2列联表,并判断有多大把握认为交通安全意识与性别有关;
(Ⅲ)在(Ⅱ)的条件下,从交通安全意识强的驾驶员中随机抽取2人,求抽到的女性人数![]() 的分布列及期望.
的分布列及期望.
附: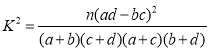 ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |