题目内容
【题目】设![]() 为实数,
为实数,![]() .证明:
.证明:
(1)把![]() 写成无穷乘积有唯一的表达式
写成无穷乘积有唯一的表达式 其中,
其中,![]() 为正整数,满足
为正整数,满足![]() ;
;
(2)![]() 是有理数,当且仅当它的无穷乘积具有下列性质:存在
是有理数,当且仅当它的无穷乘积具有下列性质:存在![]() ,对所有的
,对所有的![]() ,满足
,满足![]()
【答案】(1)见解析;(2)见解析
【解析】
(1)用归纳法来构造数列![]() 和比
和比 满足对所有的
满足对所有的![]() .
.
取![]() 为满足下列式子的最小的
为满足下列式子的最小的![]() :
:![]() .
.
因此,对于每个![]() ,
,![]() .
.
故
![]() .
.
因为![]() ,
,![]() ,所以,
,所以,![]() .
.
从而, .
.
无穷乘积的唯一性可以由在上述递推步骤中![]() 必须满足式①得到.
必须满足式①得到.
事实上,若对于某一个![]() 有
有![]() ,则
,则![]() ,
,![]() .
.
于是,![]() 就不能收敛于1.
就不能收敛于1.
注意到,对于![]() ,有
,有
![]() .②
.②
假设对于某些![]() ,有
,有![]() ,则
,则
 ,矛盾.
,矛盾.
(2)由式②,知当乘积按上述方式终止时,![]() 是有理数.
是有理数.
另一方面,设![]() 是有理数,且
是有理数,且![]() .
.
下面证明:存在![]() ,使得
,使得![]() .
.
若不然,则对于所有的![]() 有
有![]() .
.
对每一个![]() ,将
,将![]() 写成分数的形式(不必是最简形式)
写成分数的形式(不必是最简形式)![]() ,其中,
,其中,![]() ,
,![]() ,一般地,
,一般地,![]() ,
,![]() ,
,![]() 为正整数.
为正整数.
为得到矛盾,只需证明数列![]() 是严格递减的.
是严格递减的.
事实上,![]() ,
,
这是由于![]() .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
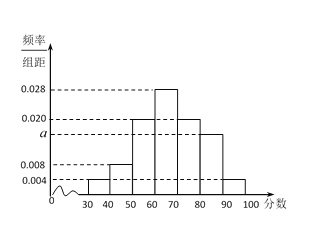
【题目】改革开放40年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各50人,进行问卷测评,所得分数的频率分布直方图如图所示.规定得分在80分以上为交通安全意识强.
安全意识强 | 安全意识不强 | 合计 | |
男性 | |||
女性 | |||
合计 |
(Ⅰ)求![]() 的值,并估计该城市驾驶员交通安全意识强的概率;
的值,并估计该城市驾驶员交通安全意识强的概率;
(Ⅱ)已知交通安全意识强的样本中男女比例为4:1,完成2×2列联表,并判断有多大把握认为交通安全意识与性别有关;
(Ⅲ)在(Ⅱ)的条件下,从交通安全意识强的驾驶员中随机抽取2人,求抽到的女性人数![]() 的分布列及期望.
的分布列及期望.
附: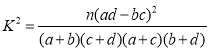 ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |