题目内容
设函数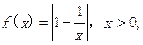
(Ⅰ) 证明: 当0< a < b ,且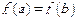 时,ab >1;
时,ab >1;
(Ⅱ) 点P (x0, y0 ) (0< x0 <1 )在曲线y=f(x)上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用x0表达).
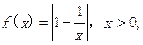
(Ⅰ) 证明: 当0< a < b ,且
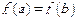 时,ab >1;
时,ab >1;(Ⅱ) 点P (x0, y0 ) (0< x0 <1 )在曲线y=f(x)上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用x0表达).
(1)见解析(2)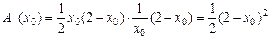
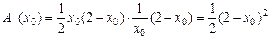
证明:(I)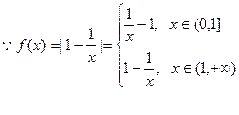
故f(x)在(0,1]上是减函数,而在(1,+∞)上是增函数,由0<a<b且f(a)=f(b)得0<a<1<b和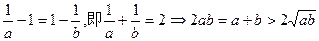
故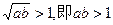
(II)0<x<1时,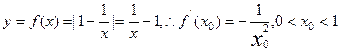
曲线y=f(x)在点P(x0,y0)处的切线方程为:
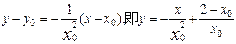
∴切线与x轴、y轴正向的交点为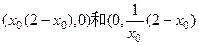
故所求三角形面积表达式为: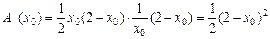
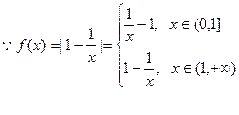
故f(x)在(0,1]上是减函数,而在(1,+∞)上是增函数,由0<a<b且f(a)=f(b)得0<a<1<b和
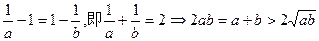
故
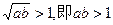
(II)0<x<1时,
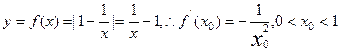
曲线y=f(x)在点P(x0,y0)处的切线方程为:
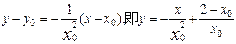
∴切线与x轴、y轴正向的交点为
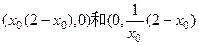
故所求三角形面积表达式为:
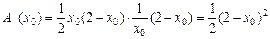

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
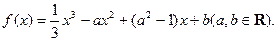
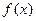 的极值点,求a的值;
的极值点,求a的值;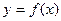 的图象在点(1,
的图象在点(1,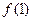 )处的切线方程为
)处的切线方程为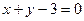 ,求
,求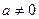 时,若
时,若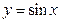 在
在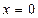 和
和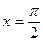 附近的平均变化率,并比较它们的大小.
附近的平均变化率,并比较它们的大小.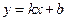 ,其中
,其中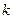 、
、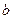
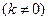 是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数
是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数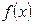 ,在点
,在点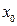 附近一点
附近一点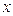 的函数值
的函数值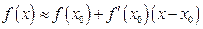 .利用这一方法,
.利用这一方法,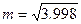 的近似代替值
的近似代替值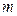
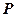 是曲线
是曲线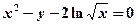 上任意一点,则点
上任意一点,则点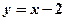 的最小距离为
的最小距离为 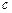 ,年产量为
,年产量为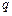 ,产品单价为
,产品单价为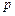 ,三者之间存在关系:
,三者之间存在关系: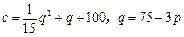 .问:应确定年产量为多少时,才能达到最大利润?此时,产品单价为多少?
.问:应确定年产量为多少时,才能达到最大利润?此时,产品单价为多少?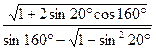 ;
;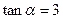 ,求
,求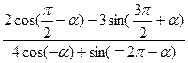 的值.
的值.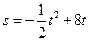 (t是时间,s是位移),则物体在时刻t=2时的
(t是时间,s是位移),则物体在时刻t=2时的 速度为 ( )
速度为 ( )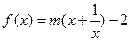 的图象与函数
的图象与函数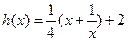 的图象关于原点对称.(1)求m的值;
的图象关于原点对称.(1)求m的值;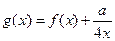 ,求
,求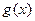 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。