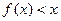题目内容
(本小题共13分)
已知函数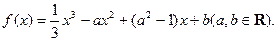
(I)若x=1为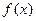 的极值点,求a的值;
的极值点,求a的值;
(II)若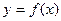 的图象在点(1,
的图象在点(1,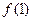 )处的切线方程为
)处的切线方程为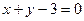 ,求
,求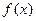 在区间[-2,4]上的最大值;
在区间[-2,4]上的最大值;
(III)当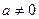 时,若
时,若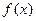 在区间(-1,1)上不单调,求a的取值范围.
在区间(-1,1)上不单调,求a的取值范围.
已知函数
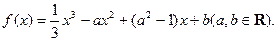
(I)若x=1为
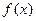 的极值点,求a的值;
的极值点,求a的值;(II)若
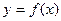 的图象在点(1,
的图象在点(1,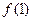 )处的切线方程为
)处的切线方程为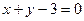 ,求
,求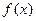 在区间[-2,4]上的最大值;
在区间[-2,4]上的最大值;(III)当
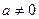 时,若
时,若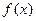 在区间(-1,1)上不单调,求a的取值范围.
在区间(-1,1)上不单调,求a的取值范围.(I)0或2
(II)8
(III)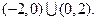
(II)8
(III)
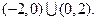
(I)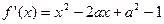
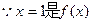 的极值点,
的极值点,
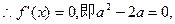
解得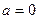 或2. …………4分
或2. …………4分
(II)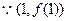 是切点,
是切点,
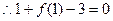
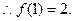
即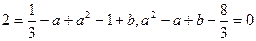
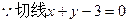 的斜率为-1
的斜率为-1
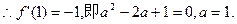
代入解得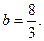
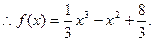
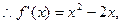
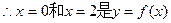 的两个极值点.
的两个极值点.
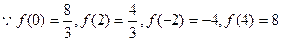
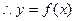 在[-2,4]上的最大值为8. …………10分
在[-2,4]上的最大值为8. …………10分
(III)因为函数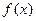 在区间(-1,1)不单调,
在区间(-1,1)不单调,
所以函数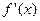 在(-1,1)上存在零点.
在(-1,1)上存在零点.
而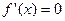 的两根为a-1,a+1,区间长为2,
的两根为a-1,a+1,区间长为2,
∴在区间(-1,1)上不可能有2个零点.
所以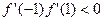
即: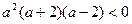
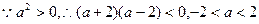
又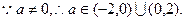 …………13分
…………13分
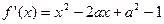
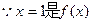 的极值点,
的极值点,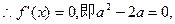
解得
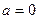 或2. …………4分
或2. …………4分(II)
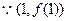 是切点,
是切点,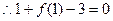
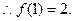
即
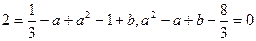
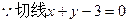 的斜率为-1
的斜率为-1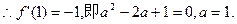
代入解得
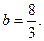
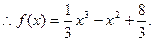
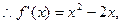
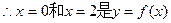 的两个极值点.
的两个极值点.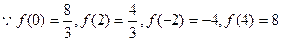
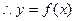 在[-2,4]上的最大值为8. …………10分
在[-2,4]上的最大值为8. …………10分(III)因为函数
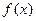 在区间(-1,1)不单调,
在区间(-1,1)不单调,所以函数
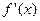 在(-1,1)上存在零点.
在(-1,1)上存在零点.而
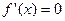 的两根为a-1,a+1,区间长为2,
的两根为a-1,a+1,区间长为2,∴在区间(-1,1)上不可能有2个零点.
所以
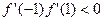
即:
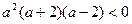
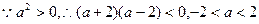
又
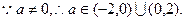 …………13分
…………13分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
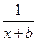 (a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3。
(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3。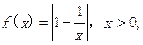
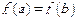 时,ab >1;
时,ab >1;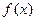 的定义域
的定义域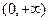 ,对于任意正实数m,n恒有
,对于任意正实数m,n恒有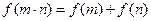 ,且当
,且当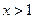 时,
时,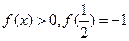 .
.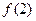 的值;(2)求证:
的值;(2)求证: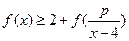 ,其中
,其中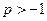 .
.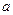
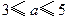
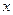
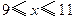
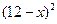
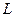 (万元)与每件产品的售价
(万元)与每件产品的售价 出
出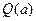
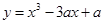 在
在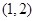 内有极小值,则实数
内有极小值,则实数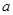 的取值范围是( )
的取值范围是( )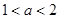
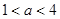
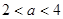

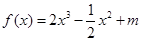 (
(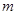 为常数)图象上
为常数)图象上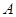 处的切线与直线
处的切线与直线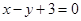 的夹角为45°,则点
的夹角为45°,则点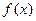 在
在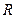 上的导函数为
上的导函数为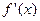 ,且
,且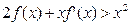 ,以下不等式恒成立的是
,以下不等式恒成立的是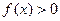 B
B 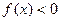 C
C 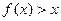 D
D