题目内容
函数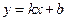 ,其中
,其中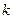 、
、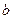
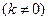 是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数
是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数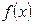 ,在点
,在点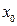 附近一点
附近一点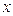 的函数值
的函数值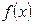 ,可以用如下方法求其近似代替值:
,可以用如下方法求其近似代替值: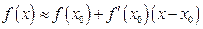 .利用这一方法,
.利用这一方法,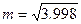 的近似代替值
的近似代替值
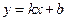 ,其中
,其中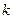 、
、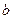
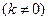 是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数
是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数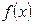 ,在点
,在点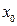 附近一点
附近一点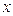 的函数值
的函数值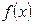 ,可以用如下方法求其近似代替值:
,可以用如下方法求其近似代替值: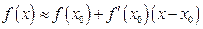 .利用这一方法,
.利用这一方法,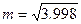 的近似代替值
的近似代替值A.大于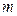 | B.小于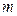 | C.等于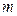 | D.与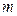 的大小关系无法确定 的大小关系无法确定 |
A
设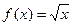 ,则
,则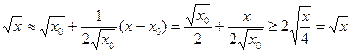 ,当且仅当
,当且仅当 时取等号,所以
时取等号,所以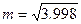 的近似代替值大于
的近似代替值大于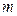 ,选择A.
,选择A.
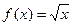 ,则
,则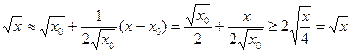 ,当且仅当
,当且仅当 时取等号,所以
时取等号,所以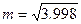 的近似代替值大于
的近似代替值大于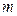 ,选择A.
,选择A.
练习册系列答案
相关题目
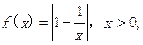
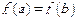 时,ab >1;
时,ab >1;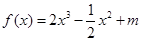 (
(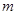 为常数)图象上
为常数)图象上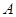 处的切线与直线
处的切线与直线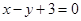 的夹角为45°,则点
的夹角为45°,则点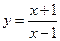 在点
在点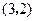 处的切线与直线
处的切线与直线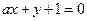 垂直,则
垂直,则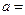 ( )
( )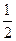
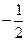
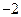
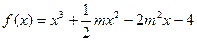 (m为常数,且m>0)有极大值
(m为常数,且m>0)有极大值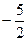 ,
,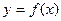 的斜率为2的切线方程.
的斜率为2的切线方程. km处的海岸渔站中,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸可以使抵达渔站的时间最省?
km处的海岸渔站中,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸可以使抵达渔站的时间最省? 。
。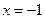 处的切线方程;
处的切线方程;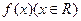 的一段图象如图所示,
的一段图象如图所示,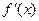 是函数
是函数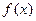 的导函数,且
的导函数,且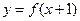 是奇函数,给出以下结论:
是奇函数,给出以下结论: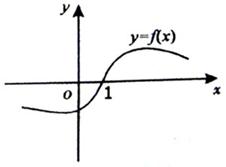
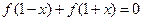 ;
;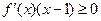 ;
;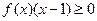 ;
;