题目内容
8.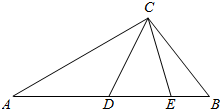 如图△ABC中,C=$\frac{π}{2}$,AC=$\sqrt{3}$,BC=1,D,E为线段AB的点,∠ACD=$\frac{π}{4}$,∠DCE=$\frac{π}{6}$,则△DCE的面积为( )
如图△ABC中,C=$\frac{π}{2}$,AC=$\sqrt{3}$,BC=1,D,E为线段AB的点,∠ACD=$\frac{π}{4}$,∠DCE=$\frac{π}{6}$,则△DCE的面积为( )| A. | $\frac{6-3\sqrt{3}}{4}$ | B. | $\frac{9-3\sqrt{3}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{3}}{8}$ |
分析 求出CD,CE,利用三角形的面积公式,即可得出结论.
解答 解:由题意,△ACD中,∠A=30°,∠ACD=45°,AC=$\sqrt{3}$,∴CD=$\frac{\sqrt{3}sin30°}{sin105°}$=$\frac{3\sqrt{2}-\sqrt{6}}{2}$,
△BCE中,∠BCE=15°,∠B=60°,∴∠DEC=75°,∴CE=CD=$\frac{3\sqrt{2}-\sqrt{6}}{2}$,
∴△DCE的面积为$\frac{1}{2}$×($\frac{3\sqrt{2}-\sqrt{6}}{2}$)2×sin30°=$\frac{6-3\sqrt{3}}{4}$.
故选:A.
点评 本题考查三角形面积的计算,考查正弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
18.已知cos($\frac{π}{3}$+α)=-$\frac{1}{3}$,则sin(α-$\frac{π}{6}$)的值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | -$\frac{2\sqrt{3}}{3}$ |
19.a、b表示两条直线,α、β、γ表示三个平面,下列命题中错误的是( )
| A. | a?α,b?α,且a∥β,b∥β,则α∥β | |
| B. | a、b是异面直线,则存在唯一的平面与a、b等距 | |
| C. | a⊥α,b?β,a⊥b,则α∥β | |
| D. | α⊥γ,γ∥β,a⊥α,b⊥β,则a⊥b |
3. 在正方体ABCD-A1B1C1D1的棱所在的直线中,与直线AB垂直的异面直线共有( )
在正方体ABCD-A1B1C1D1的棱所在的直线中,与直线AB垂直的异面直线共有( )
 在正方体ABCD-A1B1C1D1的棱所在的直线中,与直线AB垂直的异面直线共有( )
在正方体ABCD-A1B1C1D1的棱所在的直线中,与直线AB垂直的异面直线共有( )| A. | 1条 | B. | 2条 | C. | 4条 | D. | 8条 |
17.小明同学每天下午4:00到5:00之间放学到家学习,小刚同学每天下午4:30到5:30之间到达小明家给他辅导功课,则小刚到小明家时就能见到小明的概率是( )
| A. | 1 | B. | 0.875 | C. | 0.65 | D. | 0.5 |