题目内容
3．
在正方体ABCD-A1B1C1D1的棱所在的直线中，与直线AB垂直的异面直线共有（ ）| A． | 1条 | B． | 2条 | C． | 4条 | D． | 8条 |
分析 由已知条件利用垂直和异面直线的概念，结合正方体的结构特征直接求解．
解答 解：如图，在正方体ABCD-A1B1C1D1的棱所在的直线中，
与直线AB垂直的异面直线有：
DD1、CC1、A1D1，B1C1，共四条，
故选：C．
点评 本题考查异面直线的条数的求法，是基础题，解题时要注意列举法的合理运用．
练习册系列答案
相关题目
14．一菱形土地的面积为$\sqrt{3}$平方公里，菱形的最小角为60度，如果要将这一菱形土地向外扩张变成一正方形土地，问正方形土地边长最小为多少公里（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{6}$ | D． | 2$\sqrt{6}$ |
18．设抛物线的焦点为F、顶点为O、准线与对称轴的交点为K，分别过F、O、K的三条平行直线被抛物线所截得的弦长依次为a，b，c，则（ ）
| A． | a2+c2=2b2 | B． | ac=b2 | C． | a+c=2b | D． | ac=2b2 |
8．
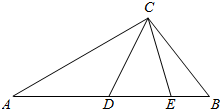如图△ABC中，C=$\frac{π}{2}$，AC=$\sqrt{3}$，BC=1，D，E为线段AB的点，∠ACD=$\frac{π}{4}$，∠DCE=$\frac{π}{6}$，则△DCE的面积为（ ）
如图△ABC中，C=$\frac{π}{2}$，AC=$\sqrt{3}$，BC=1，D，E为线段AB的点，∠ACD=$\frac{π}{4}$，∠DCE=$\frac{π}{6}$，则△DCE的面积为（ ）| A． | $\frac{6-3\sqrt{3}}{4}$ | B． | $\frac{9-3\sqrt{3}}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{\sqrt{3}}{8}$ |
12．函数f（x）=sinx+$\frac{1}{lnx}$的定义域是（ ）
| A． | （0，+∞） | B． | （e，+∞） | C． | （0，1）∪（1，+∞） | D． | （1，e）∪（e，+∞） |
13．对任意x∈（0，$\frac{π}{2}$），不等式tanx•f（x）＜f′（x）恒成立，则下列不等式错误的是（ ）
| A． | f（$\frac{π}{3}$）＞$\sqrt{2}$f（$\frac{π}{4}$） | B． | f（$\frac{π}{3}$）＞2cos1•f（1） | C． | f（$\frac{π}{4}$）＜2cos1•f（1） | D． | f（$\frac{π}{4}$）＜$\frac{\sqrt{6}}{2}$f（$\frac{π}{6}$） |